��Ŀ����
����Ŀ����һ��������һ���ߵ�ƽ�������������ߵij˻������ǰ���������ν������������Σ�
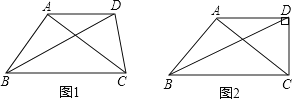
��1����֪��ABC�DZ��������Σ�AB��3��BC��4����ֱ��д����������������AC�ij���
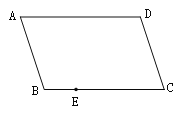
��2����ͼ1�����ı���ABCD�У�AD��BC���Խ���BDƽ�֡�ABC����BAC����ADC����֤����ABC�DZ��������Σ�
��3����ͼ2���ڣ�2���������£�����ADC��90��ʱ�����![]() ��ֵ��
��ֵ��
���𰸡�(1) 2![]() ��
��![]() ��
��![]() �������Ѿ���������
�������Ѿ���������
��������
��1�����ݱ��������εĶ����AB2��BCAC��BC2��ABAC��AC2��ABBC��������ֱ�������ɵã�
��2����֤��ABC�ס�DCA��CA2��BCAD�����ɡ�ADB����CBD����ABD֪AB��AD���ɵã�
��3����AH��BD����AB��AD֪BH��![]() BD����֤��ABH�ס�DBC��ABBC��BHDB����ABBC��
BD����֤��ABH�ס�DBC��ABBC��BHDB����ABBC��![]() BD2�����ABBC��AC2֪
BD2�����ABBC��AC2֪![]() BD2��AC2���ݴ˿ɵô𰸣�
BD2��AC2���ݴ˿ɵô𰸣�
��1����AC��m��
������m2��3��4��32��4m��42��3m��
��m��2![]() ��
��![]() ��
��![]() �������Ѿ���������
�������Ѿ���������
��2����AD��BC��
���ACB����DAC��
�ߡ�BAC����ADC��
���ADC�ס�CAB��
��![]() ��
��
��ADBC��AC2��
��AD��BC��
���CBD����ADB��
��BDƽ�֡�ABC��
���ABD����ADB��
��AB��AD��
��ABBC��AC2��
���ABC�DZ���������
��3����ͼ2�У���AH��BD��
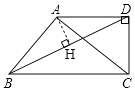
��֤��ABH�ס�DBC��
��![]() ��
��![]() ��
��
��ABBC��BHBD��
��AB��AD��AH��BD��H��
��BH��DH��![]() BD��
BD��
��BD��2BH��
��ABBC��![]() BD2��
BD2��
��ABBC��AC2��
��AC2��![]() BD2��
BD2��
��AC��0��BD��0��
��![]() ��
��![]() ��
��

 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д�