Question

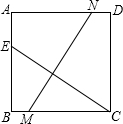（2013•宝坻区一模）如图，在正方形ABCD中，CE=MN，∠MCE=35°，那么∠ANM等于（　　）

A．45°

B．50°

C．55°

D．60°

Answer 1

分析：过B作BF∥MN交AD于F，则∠AFB=∠ANM，根据正方形的性质得出∠A=∠EBC=90°，AB=BC，AD∥BC，推出四边形BFNM是平行四边形，得出BF=MN=CE，证Rt△ABF≌Rt△BCE，推出∠AFB=∠ECB即可．

解答：解：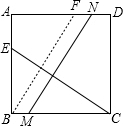
过B作BF∥MN交AD于F，
则∠AFB=∠ANM，
∵四边形ABCD是正方形，
∴∠A=∠EBC=90°，AB=BC，AD∥BC，
∴FN∥BM，BE∥MN，
∴四边形BFNM是平行四边形，
∴BF=MN，
∵CE=MN，
∴CE=BF，
在Rt△ABF和Rt△BCE中

BF=CE AB=BC

∴Rt△ABF≌Rt△BCE（HL），
∴∠AFB=∠ECB=35°，
∴∠ANM=∠AFB=35°，
故选C．

点评：本题考查了平行四边形的性质和判定，全等三角形的性质和判定，正方形的性质的应用，主要考查学生的推理能力．