Question

（2013•莆田模拟）函数y=

4

x

和y=

1

x

在第一象限内的图象如图，点P是y=

4

x

的图象上一动点，PC⊥x轴于C，交y=

1

x

的图象于点A，PD⊥y轴于D，交y=

1

x

的图象于点B．
给出如下结论：①△ODB与△OCA的面积相等；②PA与PB始终相等；③四边形PAOB的面积大小不会发生变化；④

PA

AC

=

PB

BD

．
其中所有正确结论的序号是

①③④

．

Answer 1

分析：由于A、B是反比函数y=

1

x

上的点，可得出S_△OBD=S_△OAC=

1

2

故①正确；当P的横纵坐标相等时PA=PB，故②错误；根据反比例函数系数k的几何意义可求出四边形PAOB的面积为定值，故③正确；连接PO，根据底面相同的三角形面积的比等于高的比即可得出结论．

解答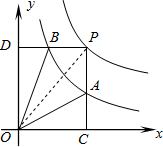：解：∵A、B是反比函数y=

1

x

上的点，
∴S_△OBD=S_△OAC=

1

2

，故①正确；
∵当P的横纵坐标相等时PA=PB，故②错误；
∵P是反比例函数y=

4

x

上的点，
∴S_矩形PDOC=4，
∴S_{四边形PAOB}=S_矩形PDOC-S_△ODB--S_△OAC=4-

1

2

-

1

2

=3，故③正确；
连接OP，
∵

S△POC

S△OAC

=

PC

AC

=

2

1 2

=4，
∴AC=

1

4

PC，PA=

3

4

PC，
∴

PA

AC

=3，
同理可得

PB

BD

=3，
∴

PA

AC

=

PB

BD

，故④正确．
故答案为：①③④

点评：本题考查的是反比例函数综合题，熟知反比例函数中系数k的几何意义是解答此题的关键．