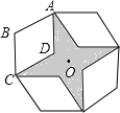
题目内容
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)、求证:四边形AODE是矩形;(2)、若AB=6,∠BCD=120°,求四边形AODE的面积.

【答案】(1)、证明过程见解析;(2)、9![]()
【解析】
试题分析:(1)、根据两组对边分别平行得出平行四边形,根据菱形的性质得出矩形;(2)、根据菱形得出△ABC为正三角形,得出OB和AO的长度,然后计算面积.
试题解析:(1)、∵四边形ABCD是菱形 ∴AC⊥BD,即∠AOD=90° ∵DE∥AC,AE∥BD
∴四边形AODE是平行四边形 ∵∠AOD=90° ∴□AODE是矩形
(2)、∵四边形ABCD是菱形 ∴AO=OC=![]() ,BO=OD,AB=BC, AB∥CD
,BO=OD,AB=BC, AB∥CD
∴∠ABC+∠BCD=180° ∵∠BCD=120° ∴∠ABC=60° ∴△ABC是等边三角形
∴AC=AB=6 ∴OA=3 根据Rt△ABO的勾股定理可得BO=3![]() 即DO=3
即DO=3![]()
∴S=AO×DO=3×3![]() =9
=9![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目