题目内容
根据二次函数y=-x2+2x+3的图象,判断下列说法中,错误的是
- A.二次函数图象的对称轴是直线x=1
- B.当x>0时,y<4
- C.当x≤1时,函数值y是随着x的增大而增大
- D.当y≥0时,x的取值范围是-1≤x≤3时
B
分析:把二次函数写成顶点式形式,再根据二次函数的对称轴,增减性对各选项分析判断后利用排除法求解.
解答:y=-x2+2x+3=-(x-1)2+4,
A、二次函数y=-x2+2x+3的对称轴为直线x=-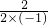 =1,故本选项错误;
=1,故本选项错误;
B、当x=1时,y最大值为4,所以x>0时,y≤4,故本选项正确;
C、当x≤1时,函数值y是随着x的增大而增大正确,故本选项错误;
D、令y=0,则-x2+2x+3=0,
即x2-2x-3=0,
解得x1=-1,x2=3,
所以,当y≥0时,x的取值范围是-1≤x≤3正确,故本选项错误.
故选B.
点评:本题考查了二次函数的性质,主要利用了对称轴解析式,二次函数的增减性,与x轴的交点坐标的求解,是基础题.
分析:把二次函数写成顶点式形式,再根据二次函数的对称轴,增减性对各选项分析判断后利用排除法求解.
解答:y=-x2+2x+3=-(x-1)2+4,
A、二次函数y=-x2+2x+3的对称轴为直线x=-
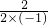 =1,故本选项错误;
=1,故本选项错误;B、当x=1时,y最大值为4,所以x>0时,y≤4,故本选项正确;
C、当x≤1时,函数值y是随着x的增大而增大正确,故本选项错误;
D、令y=0,则-x2+2x+3=0,
即x2-2x-3=0,
解得x1=-1,x2=3,
所以,当y≥0时,x的取值范围是-1≤x≤3正确,故本选项错误.
故选B.
点评:本题考查了二次函数的性质,主要利用了对称轴解析式,二次函数的增减性,与x轴的交点坐标的求解,是基础题.

练习册系列答案
相关题目
