题目内容
(2010•宁波)如图,已知⊙P的半径为2,圆心P在抛物线y=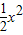 -1上运动,当⊙P与x轴相切时,圆心P的坐标为 .
-1上运动,当⊙P与x轴相切时,圆心P的坐标为 .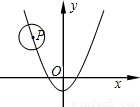
【答案】分析:当⊙P与x轴相切时,P点的纵坐标为2,可将其代入抛物线的解析式中,即可求得P点坐标.
解答:解:当⊙P与x轴相切时,P点纵坐标为±2;
当y=2时, x2-1=2,
x2-1=2,
解得x=±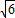 ;
;
当y=-2时, x2-1=-2,
x2-1=-2,
x无解;
故P点坐标为(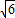 ,2)或(-
,2)或(-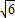 ,2).
,2).
点评:能够判断出⊙P与x轴相切时P点的纵坐标,是解答此题的关键.
解答:解:当⊙P与x轴相切时,P点纵坐标为±2;
当y=2时,
 x2-1=2,
x2-1=2,解得x=±
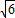 ;
;当y=-2时,
 x2-1=-2,
x2-1=-2,x无解;
故P点坐标为(
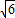 ,2)或(-
,2)或(-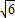 ,2).
,2).点评:能够判断出⊙P与x轴相切时P点的纵坐标,是解答此题的关键.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
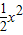 -1上运动,当⊙P与x轴相切时,圆心P的坐标为 .
-1上运动,当⊙P与x轴相切时,圆心P的坐标为 .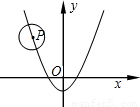
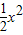 +bx+c的图象经过A(2,0)、B(0,-6)两点.
+bx+c的图象经过A(2,0)、B(0,-6)两点.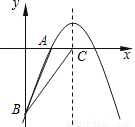
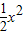 -1上运动,当⊙P与x轴相切时,圆心P的坐标为 .
-1上运动,当⊙P与x轴相切时,圆心P的坐标为 .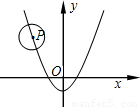
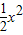 -1上运动,当⊙P与x轴相切时,圆心P的坐标为 .
-1上运动,当⊙P与x轴相切时,圆心P的坐标为 .