题目内容
1、若两个相似三角形的相似比是2：3，则它们的对应高线的比是
2：3
，对应中线的比是2：3
，对应角平分线的比是2：3
，周长比是2：3
，面积比是4：9
．分析：相似三角形的相似比等于其对应高的比，对应中线的比，角平分线的比，周长的比，其面积比等于相似比的平方．
解答：解：由于相似三角形的相似比是2：3，
则其对应高的比，对应中线的比，角平分线的比，周长的比都等于其相似比，
即2：3，
面积比等于相似比的平方，即4：9．
故答案为：2：3；2：3；2：3；2：3；4：9．
则其对应高的比，对应中线的比，角平分线的比，周长的比都等于其相似比，
即2：3，
面积比等于相似比的平方，即4：9．
故答案为：2：3；2：3；2：3；2：3；4：9．
点评：本题主要考查了相似三角形的性质问题，即相似比与高，中线，角平分线，周长及面积的关系．
练习册系列答案
全能测控一本好卷系列答案
相关题目
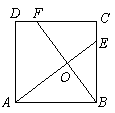
25、如图，有两个动点E，F分别从正方形ABCD的两个顶点B，C同时出发，以相同速度分别沿边BC和CD移动，问：
分别从正方形
的两个顶点
同时出发，以相同速度分别沿边
和
移动，问：
与
的位置和大小有何关系？并给予证明．
，图中有多少对相似三角形？请把它们写出来．
