题目内容
(1998•绍兴)已知:如图,△ABC中,点D、E分别在AB、AC上,DE∥BC,过A、D、C点的圆交DE的延长线于F.求证:△FCE∽△ABC.
【答案】分析:根据平行线可以得到∠FDA=∠B,根据同弧上所对的圆周角相等可以得到∠A=∠F,∠FCE=∠FDA.然后就可以证明题目结论了.
解答:证明:∵DE∥BC,
∴∠FDA=∠B.
而∠A=∠F,∠FCE=∠FDA,
∴∠FCE=∠B.
∴△FCE∽△ABC.
点评:此题比较简单,利用平行线的性质和同弧上的圆周角相等就可以得到角的关系,然后利用了相似三角形的判定可证明结论.
解答:证明:∵DE∥BC,
∴∠FDA=∠B.
而∠A=∠F,∠FCE=∠FDA,
∴∠FCE=∠B.
∴△FCE∽△ABC.
点评:此题比较简单,利用平行线的性质和同弧上的圆周角相等就可以得到角的关系,然后利用了相似三角形的判定可证明结论.

练习册系列答案
相关题目


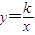 上有两点A(x1,y1)、B(x2,y2),若x2<x1<0,则y1与y2的大小关系是( )
上有两点A(x1,y1)、B(x2,y2),若x2<x1<0,则y1与y2的大小关系是( )