题目内容
 问题情境
问题情境
要围成面积为36cm2的长方形,当该长方形的长为多少时,它的周长最小?最小值是多少?
数学模型
设长方形的面积为s(s>0),长为x(x>0),周长为y,则y与x的函数关系式为______
探索研究
(1)我们可以借鉴研究函数的经验,先探索s=1时的函数的图象性质.
①填写下表,画出函数的图象;
| x |  |  |  |  | 1 | 2 | 3 | 4 | 5 |
| y |
(2)在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到,请你通过配方求“数学模型”中函数的最小值.
解决问题
用上述方法解决“问题情境”中的问题,直接写出答案.
解:∵设长方形的面积为s(s>0),长为x(x>0),周长为y,
∴长方形的宽为: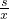 ,
,
则y与x的函数关系式为:y=2(x+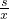 );
);
故答案为:y=2(x+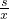 );
);
(1)①由题意得出:y=2(x+ ),
),
如图所示:
 ;
;
②当0<x<1时,y随x的增大而减少;
当x>1时,y随x的增大而增大;
当x=1时,y有最小值4;
(2)y=2(x+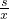 )
)
=2[( )2+(
)2+( )2]
)2]
=2( -
- )2+4
)2+4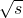 .
.
当 -
- =0,即x=
=0,即x=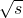 时,y有最小值4
时,y有最小值4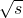 ;
;
解决问题:
当x= =6(cm)时,y有最小值4
=6(cm)时,y有最小值4 =24(cm).
=24(cm).
分析:数学模型:利用长方形的面积为s(s>0),长为x(x>0),表示出长方形的宽,进而得出y与x的关系式;
探索研究:(1)①利用s=1代入,进而求出x与y的对应值,画出图象即可;
②利用图象直接分析函数增减性即可;
(2)利用配方法求出函数最值即可;
解决问题:利用(2)所求直接得出答案即可.
点评:此题主要考查了函数的应用以及函数图象的画法和函数增减性以及函数最值问题,利用数形结合得出是解题关键.
∴长方形的宽为:
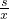 ,
,则y与x的函数关系式为:y=2(x+
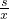 );
);故答案为:y=2(x+
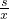 );
);(1)①由题意得出:y=2(x+
 ),
),| x |  |  |  |  | 1 | 2 | 3 | 4 | 5 |
| y | 10 | 8 | 6 | 5 | 4 | 5 | 6 | 8 | 10 |
 ;
;②当0<x<1时,y随x的增大而减少;
当x>1时,y随x的增大而增大;
当x=1时,y有最小值4;
(2)y=2(x+
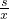 )
)=2[(
 )2+(
)2+( )2]
)2]=2(
 -
- )2+4
)2+4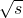 .
.当
 -
- =0,即x=
=0,即x=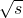 时,y有最小值4
时,y有最小值4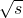 ;
;解决问题:
当x=
 =6(cm)时,y有最小值4
=6(cm)时,y有最小值4 =24(cm).
=24(cm).分析:数学模型:利用长方形的面积为s(s>0),长为x(x>0),表示出长方形的宽,进而得出y与x的关系式;
探索研究:(1)①利用s=1代入,进而求出x与y的对应值,画出图象即可;
②利用图象直接分析函数增减性即可;
(2)利用配方法求出函数最值即可;
解决问题:利用(2)所求直接得出答案即可.
点评:此题主要考查了函数的应用以及函数图象的画法和函数增减性以及函数最值问题,利用数形结合得出是解题关键.

练习册系列答案
相关题目