题目内容
如图，已知⊙O的两条弦AC，BD相交于点E，∠A=70°，∠C=50°，则sin∠AEB=分析：先由圆周角定理及∠C=50°求出∠B的度数，再由三角形内角和定理求∠AEB的度数，根据特殊角的三角函数值解答即可．
解答：解：∵∠C=50°，∴∠B=∠C=50°，
∵∠A=70°，
∴∠AEB=180°-∠B-∠A=180°-70°-50°=60°．
∴sin∠AEB=sin60°=
．
∵∠A=70°，
∴∠AEB=180°-∠B-∠A=180°-70°-50°=60°．
∴sin∠AEB=sin60°=
| ||
| 2 |
点评：本题比较简单，考查的是圆周角定理及特殊角的三角函数值．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
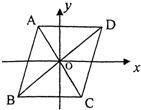9、如图，已知?ABCD的两条对角线AC与BD交于平面直角坐标系的原点，点A的坐标为（-2，3），则点C的坐标为（ ）
15、如图，已知△ABC的两条角平分线BE、CF相交于点D，∠A=40°，则∠BDC=
如图，已知⊙O的两条弦AC，BD相交于点E，∠A=70°，∠C=50°，那么cos∠AEB的值为（ ）
如图，已知△ABC的两条高线BD、CE相交于点O，且BE=EC．求证：BO=AC．