题目内容
如图,某小区要修建一块矩形绿地ABCD,设矩形绿地ABCD的边AD长为x米,边AB的长为y米,且y≤x.(1)如果用24米长的围栏来建绿地的边框(即矩形ABCD的周长)x,求出y与x之间的函数关系式,并直接写出自变量x的取值范围;
(2)在(1)的条件下,根据小区的规划要求,所修建的矩形绿地ABCD面积必须是32平方来,则矩形的长和宽AD、DC各为多少米?

【答案】分析:(1)根据矩形的周长公式建立等量关系,然后将y表示出来就可以了.
(2)根据矩形的面积公式建立方程x(12-x)=32,再解答这个方程就可以求出x的值,根据第(1)问的结论自变量的取值范围,就可以求出AD、DC的值.
解答:解:(1)依题意得:2(x+y)=24
y=12-x
x的取值范围是6≤x<12
(2)依题意得:S=AB•BC=x(12-x),
∴x(12-x)=32,
∴x2-12x+32=0,
解得x1=4,x2=8
∵6≤x<12∴x1=4不合题意舍去,
当x=8,y=12-x=4
答:矩形的边长为8米和4米
点评:本题考查了根据实际问题列一次函数关系式的运用,一元二次方程的运用.在解答中要注意一次函数在实际问题中自变量的取值范围的正确取舍.
(2)根据矩形的面积公式建立方程x(12-x)=32,再解答这个方程就可以求出x的值,根据第(1)问的结论自变量的取值范围,就可以求出AD、DC的值.
解答:解:(1)依题意得:2(x+y)=24
y=12-x
x的取值范围是6≤x<12
(2)依题意得:S=AB•BC=x(12-x),
∴x(12-x)=32,
∴x2-12x+32=0,
解得x1=4,x2=8
∵6≤x<12∴x1=4不合题意舍去,
当x=8,y=12-x=4
答:矩形的边长为8米和4米
点评:本题考查了根据实际问题列一次函数关系式的运用,一元二次方程的运用.在解答中要注意一次函数在实际问题中自变量的取值范围的正确取舍.

练习册系列答案
相关题目
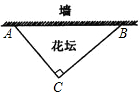 的边长各为多少米?
的边长各为多少米?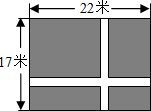 列方程解应用题:
列方程解应用题: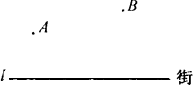
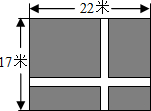 列方程解应用题:
列方程解应用题: 的边长各为多少米?
的边长各为多少米?