题目内容
(2008•河北)研究所对某种新型产品的产销情况进行了研究,为投资商在甲、乙两地生产并销售该产品提供了如下成果:第一年的年产量为x(吨)时,所需的全部费用y(万元)与x满足关系式y=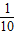 x2+5x+90,投入市场后当年能全部售出,且在甲、乙两地每吨的售价p甲,p乙(万元)均与x满足一次函数关系.(注:年利润=年销售额-全部费用)
x2+5x+90,投入市场后当年能全部售出,且在甲、乙两地每吨的售价p甲,p乙(万元)均与x满足一次函数关系.(注:年利润=年销售额-全部费用)(1)成果表明,在甲地生产并销售x吨时,P甲=-
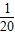 x+14,请你用含x的代数式表示甲地当年的年销售额,并求年利润W甲(万元)与x之间的函数关系式;
x+14,请你用含x的代数式表示甲地当年的年销售额,并求年利润W甲(万元)与x之间的函数关系式;(2)成果表明,在乙地生产并销售x吨时,P乙=-
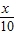 +n(n为常数),且在乙地当年的最大年利润为35万元.试确定n的值;
+n(n为常数),且在乙地当年的最大年利润为35万元.试确定n的值;(3)受资金、生产能力等多种因素的影响,某投资商计划第一年生产并销售该产品18吨,根据(1),(2)中的结果,请你通过计算帮他决策,选择在甲地还是乙地产销才能获得较大的年利润?
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是
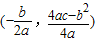 .
.
【答案】分析:依据年利润=年销售额-全部费用即可求得利润W甲(万元)与x之间的函数关系式及利润W乙(万元)与x之间的函数关系式,分别求出x=18时,W甲和W乙的值,通过比较W甲和W乙大小就可以帮助投资商做出选择.
解答:解:(1)甲地当年的年销售额为(- x+14)•x=(-
x+14)•x=(- x2+14x)万元;
x2+14x)万元;
w甲=(- x2+14x)-(
x2+14x)-( x2+5x+90)=-
x2+5x+90)=- x2+9x-90.
x2+9x-90.
(2)在乙地区生产并销售时,
年利润:
w乙=- x2+nx-(
x2+nx-( x2+5x+90)
x2+5x+90)
=- x2+(n-5)x-90.
x2+(n-5)x-90.
由 =
= ,
,
解得n=15或-5.
经检验,n=-5不合题意,舍去,
∴n=15.
(3)在乙地区生产并销售时,年利润
w乙=- x2+10x-90,
x2+10x-90,
将x=18代入上式,得w乙=25.2(万元);
将x=18代入w甲=- x2+9x-90,
x2+9x-90,
得w甲=23.4(万元).
∵W乙>W甲,
∴应选乙地.
点评:本题是一道最佳方案选择题,通过计算、比较同一个自变量的两个函数值的大小来选择最佳方案.
依据年利润=年销售额-全部费用即可求得利润W甲(万元)与x之间的函数关系式及利润W乙(万元)与x之间的函数关系式,分别求出x=18时,W甲和W乙的值,通过比较W甲和W乙大小就可以帮助投资商做出选择.
解答:解:(1)甲地当年的年销售额为(-
 x+14)•x=(-
x+14)•x=(- x2+14x)万元;
x2+14x)万元;w甲=(-
 x2+14x)-(
x2+14x)-( x2+5x+90)=-
x2+5x+90)=- x2+9x-90.
x2+9x-90.(2)在乙地区生产并销售时,
年利润:
w乙=-
 x2+nx-(
x2+nx-( x2+5x+90)
x2+5x+90)=-
 x2+(n-5)x-90.
x2+(n-5)x-90.由
 =
= ,
,解得n=15或-5.
经检验,n=-5不合题意,舍去,
∴n=15.
(3)在乙地区生产并销售时,年利润
w乙=-
 x2+10x-90,
x2+10x-90,将x=18代入上式,得w乙=25.2(万元);
将x=18代入w甲=-
 x2+9x-90,
x2+9x-90,得w甲=23.4(万元).
∵W乙>W甲,
∴应选乙地.
点评:本题是一道最佳方案选择题,通过计算、比较同一个自变量的两个函数值的大小来选择最佳方案.
依据年利润=年销售额-全部费用即可求得利润W甲(万元)与x之间的函数关系式及利润W乙(万元)与x之间的函数关系式,分别求出x=18时,W甲和W乙的值,通过比较W甲和W乙大小就可以帮助投资商做出选择.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

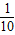 x2+5x+90,投入市场后当年能全部售出,且在甲、乙两地每吨的售价p甲,p乙(万元)均与x满足一次函数关系.(注:年利润=年销售额-全部费用)
x2+5x+90,投入市场后当年能全部售出,且在甲、乙两地每吨的售价p甲,p乙(万元)均与x满足一次函数关系.(注:年利润=年销售额-全部费用)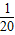 x+14,请你用含x的代数式表示甲地当年的年销售额,并求年利润W甲(万元)与x之间的函数关系式;
x+14,请你用含x的代数式表示甲地当年的年销售额,并求年利润W甲(万元)与x之间的函数关系式;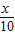 +n(n为常数),且在乙地当年的最大年利润为35万元.试确定n的值;
+n(n为常数),且在乙地当年的最大年利润为35万元.试确定n的值;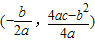 .
. x2+5x+90,投入市场后当年能全部售出,且在甲、乙两地每吨的售价p甲,p乙(万元)均与x满足一次函数关系.(注:年利润=年销售额-全部费用)
x2+5x+90,投入市场后当年能全部售出,且在甲、乙两地每吨的售价p甲,p乙(万元)均与x满足一次函数关系.(注:年利润=年销售额-全部费用) x+14,请你用含x的代数式表示甲地当年的年销售额,并求年利润W甲(万元)与x之间的函数关系式;
x+14,请你用含x的代数式表示甲地当年的年销售额,并求年利润W甲(万元)与x之间的函数关系式; +n(n为常数),且在乙地当年的最大年利润为35万元.试确定n的值;
+n(n为常数),且在乙地当年的最大年利润为35万元.试确定n的值; .
. x2+5x+90,投入市场后当年能全部售出,且在甲、乙两地每吨的售价p甲,p乙(万元)均与x满足一次函数关系.(注:年利润=年销售额-全部费用)
x2+5x+90,投入市场后当年能全部售出,且在甲、乙两地每吨的售价p甲,p乙(万元)均与x满足一次函数关系.(注:年利润=年销售额-全部费用) x+14,请你用含x的代数式表示甲地当年的年销售额,并求年利润W甲(万元)与x之间的函数关系式;
x+14,请你用含x的代数式表示甲地当年的年销售额,并求年利润W甲(万元)与x之间的函数关系式; +n(n为常数),且在乙地当年的最大年利润为35万元.试确定n的值;
+n(n为常数),且在乙地当年的最大年利润为35万元.试确定n的值; .
.