Question

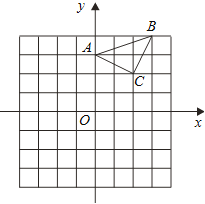
【题目】边长为2的正方形ABCD在平面直角坐标系中如图放置，已知点A的横坐标为1，作直线OC与边AD交于点E.

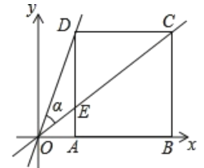
(1)求∠OCB的正弦值和余弦值;

(2)过O、D两点作直线，记该直线与直线OC的夹角为 ，试求tan的值.

Answer 1

【答案】（1）sin∠OCB=，cos∠OCB=；（2）.

【解析】

（1）由正方形的边长和A点横坐标可得出OB、BC的长，然后在Rt△OBC中利用勾股定理求出OC，根据正弦与余弦的定义即可求解；

（2）过D作DH⊥OC于H，根据相似三角形的性质得到，求出AE，DE，采用面积法可求出DH，然后利用勾股定理求出OD，OH，最后根据正切的定义即可求值.

解：（1）∵正方形ABCD的边长为2，A点横坐标为1

∴OB=1+2=3，BC=2

∴

∴sin∠OCB=

cos∠OCB=

（2）如图，过D作DH⊥OC于H，

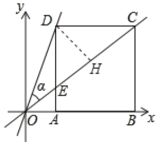
∵AD∥BC，

∴△OAE∽△OBC，

，即

∴AE=，

∴DE=，

∴CE=，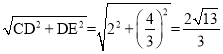

∴，

在Rt△ADO中, ，

∴，

∴.