题目内容
设a>b,则下列不等式不正确的是( )
| A、a+c>b+c | ||||
| B、a-c>b-c | ||||
C、
| ||||
| D、-2a>-2b |
分析:可分别根据不等式的基本性质对四个选项进行逐一分析,A、C可根据不等式的基本性质1解答;C可根据不等式的基本性质2解答;D可根据不等式的基本性质3解答.
解答:解:A、∵a>b,∴a+c>b+c,故本选项正确;
B、∵a>b,∴a-c>b-c,故本选项正确;
C、∵a>b,∴
>
,故本选项正确;
D、∵a>b,∴2a>2b,-2a<-2b,故本选项错误.
故选D.
B、∵a>b,∴a-c>b-c,故本选项正确;
C、∵a>b,∴
| a |
| 2 |
| b |
| 2 |
D、∵a>b,∴2a>2b,-2a<-2b,故本选项错误.
故选D.
点评:本题考查的是不等式的基本性质,熟知不等式的基本性质是解答此题的关键:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变;
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变;
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
相关题目
设a=
,b=
,c=
,则下列不等关系中正确的是( )
| 1998 |
| 1999 |
| 1999 |
| 2000 |
| 2000 |
| 2001 |
| A、a<b<c |
| B、a<c<b |
| C、b<c<a |
| D、c<b<a |
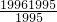 ,b=
,b=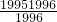 ,c=
,c= ,d=
,d=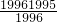 ,则下列不等关系中成立的是
,则下列不等关系中成立的是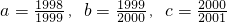 ,则下列不等关系中正确的是
,则下列不等关系中正确的是