题目内容
在△ABC中,∠B与∠C的角平分线交于O点,若∠A=50°,则∠BOC=
- A.130°
- B.50°
- C.25°
- D.115°
D
分析:根据三角形内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠OBC+∠OCB,然后在△BOC中,利用三角形的内角和定理列式进行计算即可得解.
解答: 解:∵∠A=50°,
解:∵∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,
∵∠B与∠C的角平分线交于O点,
∴∠OBC+∠OCB= (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ×130°=65°,
×130°=65°,
在△BOC中,∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°.
故选D.
点评:本题考查了三角形的内角和定理,三角形角平分线的定义,整体思想的利用是解题的关键.
分析:根据三角形内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠OBC+∠OCB,然后在△BOC中,利用三角形的内角和定理列式进行计算即可得解.
解答:
 解:∵∠A=50°,
解:∵∠A=50°,∴∠ABC+∠ACB=180°-50°=130°,
∵∠B与∠C的角平分线交于O点,
∴∠OBC+∠OCB=
 (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ×130°=65°,
×130°=65°,在△BOC中,∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°.
故选D.
点评:本题考查了三角形的内角和定理,三角形角平分线的定义,整体思想的利用是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
 25、如图,在△ABC中,AB与AC边上的高BE和CF交于点O,∠A=70°,求∠ABE和∠BOC的度数.
25、如图,在△ABC中,AB与AC边上的高BE和CF交于点O,∠A=70°,求∠ABE和∠BOC的度数.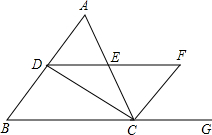 如图,在△ABC中,CD与CF分别是△ABC的内角、外角平分线,DF∥BC交AC于点E.试说明:
如图,在△ABC中,CD与CF分别是△ABC的内角、外角平分线,DF∥BC交AC于点E.试说明: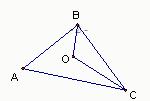 19、如图,在△ABC中,∠ACB与∠ABC的角平分线相交于点O,若∠ABC=100°,∠A=50°,那么∠BOC的度数是
19、如图,在△ABC中,∠ACB与∠ABC的角平分线相交于点O,若∠ABC=100°,∠A=50°,那么∠BOC的度数是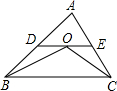 (2012•海南)如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=4,则△ADE的周长是
(2012•海南)如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=4,则△ADE的周长是 如图,在△ABC中,∠B与∠C的平分线交于点O,过O点作DE∥BC,分别交于AB、AC于D、E.若AB=7,AC=5.则△ADE的周长是
如图,在△ABC中,∠B与∠C的平分线交于点O,过O点作DE∥BC,分别交于AB、AC于D、E.若AB=7,AC=5.则△ADE的周长是