题目内容
若a为实数，则整数a2（a2-1）-a2+1的值
- A.不是负数
- B.恒为正数
- C.恒为负数
- D.不等于0
A
分析：所求式子提取公因式后化为完全平方式，根据完全平方式大于等于0，得到其值不是负数．
解答：∵a2（a2-1）-a2+1=a2（a2-1）-（a2-1）=（a2-1）2≥0，
∴a2（a2-1）-a2+1的值不是负数．
故选A
点评：此题考查了因式分解的应用，将所求式子进行适当的变形是解本题的关键．
分析：所求式子提取公因式后化为完全平方式，根据完全平方式大于等于0，得到其值不是负数．
解答：∵a2（a2-1）-a2+1=a2（a2-1）-（a2-1）=（a2-1）2≥0，
∴a2（a2-1）-a2+1的值不是负数．
故选A
点评：此题考查了因式分解的应用，将所求式子进行适当的变形是解本题的关键．
练习册系列答案
金钥匙试卷系列答案
相关题目
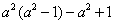的值