题目内容
在同一坐标系中，其图象与y=2x2的图象关于x轴对称的函数为
- A.y=
x2 - B.y=
x2 - C.y=-2x2
- D.y=-x2
C
分析：平面直角坐标系中任意一点P（x，y），关于x轴的对称点的坐标是（x，-y），因而用-y代替y，x不变，代入解析式就得到与y=2x2的图象关于x轴对称的函数．
解答：所求抛物线与已知抛物线y=2x2的图象顶点相同，开口大小相同，只有开口方向相反，故它们的二次项系数互为相反数，即y=-2x2．
故选C．
点评：本题主要考查了直角坐标系中关于原点对称的点的坐标的关系．
分析：平面直角坐标系中任意一点P（x，y），关于x轴的对称点的坐标是（x，-y），因而用-y代替y，x不变，代入解析式就得到与y=2x2的图象关于x轴对称的函数．
解答：所求抛物线与已知抛物线y=2x2的图象顶点相同，开口大小相同，只有开口方向相反，故它们的二次项系数互为相反数，即y=-2x2．
故选C．
点评：本题主要考查了直角坐标系中关于原点对称的点的坐标的关系．
练习册系列答案
相关题目
在同一坐标系中，其图象与y=2x2的图象关于x轴对称的函数为（ ）
A、y=
| ||
B、y=-
| ||
| C、y=-2x2 | ||
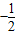| D、y=-x2 |
x2
x2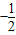
x2
x2