题目内容
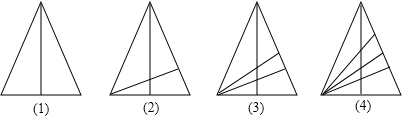
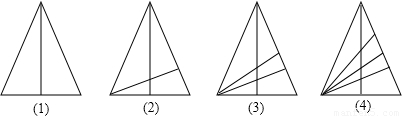
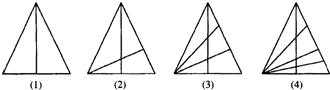
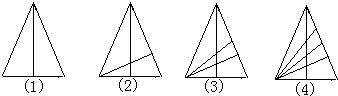
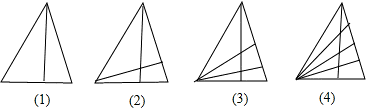
如果依次用a1，a2，a3，a4分别表示图3中（1）、（2）、（3）、（4）内三角形的个数，那么a1=3．a2=8，a3=15．a4=
24
24
．分析：可以将图（1）到图（4），看成△ABC1→△ABC2→△ABC3→△ABC4的变化过程，然后比较图（3）到图（4）的变化过程，可得出新增加的三角形个数，然后与图（3）中三角形的个数相加即可．
解答：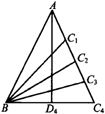
解：从图（1）到图（4），可以看成△ABC1→△ABC2→△ABC3→△ABC4的变化过程，
比较图（4）与图（3），增加的三角形中，以BD4为底得有4个，以BC4为底的也有4个，
以D4C4为底得有1个，
所以，a4=a3+2×4+1=24．
故答案为：24．
解：从图（1）到图（4），可以看成△ABC1→△ABC2→△ABC3→△ABC4的变化过程，比较图（4）与图（3），增加的三角形中，以BD4为底得有4个，以BC4为底的也有4个，
以D4C4为底得有1个，
所以，a4=a3+2×4+1=24．
故答案为：24．
点评：对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目中的难点．
练习册系列答案
相关题目
那么a1=3．a2=8，a3=15．a4=________．
