题目内容
某房地产开发公司计划建A、B两种户型的住房共80套,已知该公司所筹集的资金不少于2090万元,但不超过2096万元,且所筹集资金全部用于建房,两种户型的建房成本和售价如下表:
(1)试求该公司对这两种户型住房将有哪几种建房方案;
(2)试问该公司将如何建房,才能使获得的利润最大;
(3)若根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会提高a万元(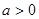 ),且所建的两种住房可全部售出.试问该公司又将如何建房,才能使获得的利润最大。(注:利润=售价-成本)
),且所建的两种住房可全部售出.试问该公司又将如何建房,才能使获得的利润最大。(注:利润=售价-成本)
| 户型 | A | B |
| 成本(万元/套) | 25 | 28 |
| 售价(万元/套) | 30 | 34 |
(2)试问该公司将如何建房,才能使获得的利润最大;
(3)若根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会提高a万元(
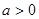 ),且所建的两种住房可全部售出.试问该公司又将如何建房,才能使获得的利润最大。(注:利润=售价-成本)
),且所建的两种住房可全部售出.试问该公司又将如何建房,才能使获得的利润最大。(注:利润=售价-成本)(1)三种建房方案:① A户型:48套,B户型32套;② A户型:49套,B户型31套;③ A户型:50套,B户型30套。(2)建48套A户型,32套B户型时获利最大(3)当5+a﹤6,即a﹤1时,方案一获利最大; 当5+a=6, 即a=1时,三种方案获利一样多; 当5+a﹥6,即a﹥1时,方案三获利最大。
解:(1)设公司建A户型x套,则建B户型(80-x)套,
由题意得: 2090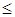 25x+28(80-x )
25x+28(80-x ) 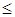 2096
2096
解得:48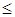 x
x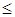 50 经检验,符合题意。
50 经检验,符合题意。
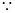 x取整数,
x取整数,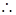 x=48、49、50。
x=48、49、50。
 该公司有以下三种建房方案:
该公司有以下三种建房方案:
①A户型:48套,B户型32套;② A户型:49套,B户型31套;
③A户型:50套,B户型30套。
(2) 每套A户型获利:30—25=5万元,
每套A户型获利:30—25=5万元,
每套B户型获利:34—28=6万元。
 每套B户型获利﹥每套A户型获利,方案一获利最大。
每套B户型获利﹥每套A户型获利,方案一获利最大。
即建48套A户型,32套B户型时获利最大。
(3)由题意得:A户型住房的售价提高a万元后:
每套A户型获利(5+a)万元,每套B户型仍获利6万元。
 当5+a﹤6,即a﹤1时,方案一获利最大;
当5+a﹤6,即a﹤1时,方案一获利最大;
当5+a=6, 即a=1时,三种方案获利一样多;
当5+a﹥6,即a﹥1时,方案三获利最大。
(1)首先设A种户型的住房建x套,则B种户型的住房建(80-x)套,然后根据题意列方程组,解方程组可求得x的取值范围,又由x取非负整数,即可求得x的可能取值,则可得到三种建房方案;
(2)求出每套户型的获利,进行比较
(3)因为a是不确定的值了,所以要根据a的取值判断该公司又将如何建房获得利润最大.
由题意得: 2090
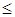 25x+28(80-x )
25x+28(80-x ) 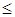 2096
2096解得:48
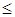 x
x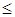 50 经检验,符合题意。
50 经检验,符合题意。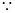 x取整数,
x取整数,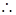 x=48、49、50。
x=48、49、50。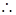 该公司有以下三种建房方案:
该公司有以下三种建房方案:①A户型:48套,B户型32套;② A户型:49套,B户型31套;
③A户型:50套,B户型30套。
(2)
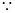 每套A户型获利:30—25=5万元,
每套A户型获利:30—25=5万元,每套B户型获利:34—28=6万元。
 每套B户型获利﹥每套A户型获利,方案一获利最大。
每套B户型获利﹥每套A户型获利,方案一获利最大。即建48套A户型,32套B户型时获利最大。
(3)由题意得:A户型住房的售价提高a万元后:
每套A户型获利(5+a)万元,每套B户型仍获利6万元。
 当5+a﹤6,即a﹤1时,方案一获利最大;
当5+a﹤6,即a﹤1时,方案一获利最大;当5+a=6, 即a=1时,三种方案获利一样多;
当5+a﹥6,即a﹥1时,方案三获利最大。
(1)首先设A种户型的住房建x套,则B种户型的住房建(80-x)套,然后根据题意列方程组,解方程组可求得x的取值范围,又由x取非负整数,即可求得x的可能取值,则可得到三种建房方案;
(2)求出每套户型的获利,进行比较
(3)因为a是不确定的值了,所以要根据a的取值判断该公司又将如何建房获得利润最大.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 的自然数解,求 可能表示的数字。
的自然数解,求 可能表示的数字。 的不等式
的不等式 的整数解共有4个,则
的整数解共有4个,则 的取值范围是( )
的取值范围是( )



 并在所给的数轴上表示出其解集.
并在所给的数轴上表示出其解集.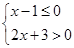 的整数解为 .
的整数解为 . ;(2)解不等式组:
;(2)解不等式组: 。
。 的解集是
的解集是 ,则
,则
