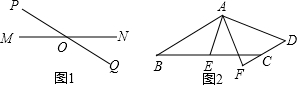题目内容
操作:如图1,点O为线段MN的中点,直线PQ与MN相交于点O,请利用图1画出一对以点O为对称中心的全等三角形.探究:如图2,在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F.试探究线段AB与AF、
FC之间的等量关系,并证明你的结论.
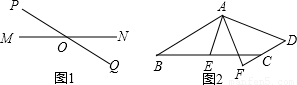
【答案】分析:(1)根据全等三角形的判定中的边角边为作图的理论依据,来画出全等三角形.
(2)本题可通过作辅助线将AB,FC,AF构建到一个相关联的三角形中,可延长AE、DF交于点M,不难证明△ABE≌△MCE,那么AB=CF,现在只要将AF也关联到三角形BEC中,我们发现,∠BAE=∠EAF,∠BAE=∠M(AB∥CD),那么三角形AMF就是个等腰三角形,AF=MF,因此AB=MC=MF+FC=AF+FC.
解答: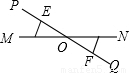 解:(1)在直线PQ上,取线段OE=OF,OM=ON,∠MOE=∠NOF,如下所示:
解:(1)在直线PQ上,取线段OE=OF,OM=ON,∠MOE=∠NOF,如下所示:
则△MOE≌△NOF.
(2)结论:AB=AF+FC;
证明过程,具体如下:
证明:延长AE交DF的延长线于点M,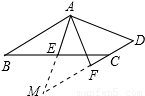
∵E为BC的中点,∴BE=CE,
∵AB∥CD,∴∠BAE=∠M,
∵∠AEB=∠MEC,∴△ABE≌△MCE,
∴AB=MC,
∵∠BAE=∠EAF,∴∠EAF=∠M.
∴MF=AF,
∵MC=MF+CF,∴AB=AF+FC.
点评:本题主要考查了相似三角形的判定和性质,等腰三角形的性质的知识点.题中作图的理论依据是全等三角形的判定中的边角边.
(2)本题可通过作辅助线将AB,FC,AF构建到一个相关联的三角形中,可延长AE、DF交于点M,不难证明△ABE≌△MCE,那么AB=CF,现在只要将AF也关联到三角形BEC中,我们发现,∠BAE=∠EAF,∠BAE=∠M(AB∥CD),那么三角形AMF就是个等腰三角形,AF=MF,因此AB=MC=MF+FC=AF+FC.
解答:
 解:(1)在直线PQ上,取线段OE=OF,OM=ON,∠MOE=∠NOF,如下所示:
解:(1)在直线PQ上,取线段OE=OF,OM=ON,∠MOE=∠NOF,如下所示:则△MOE≌△NOF.
(2)结论:AB=AF+FC;
证明过程,具体如下:
证明:延长AE交DF的延长线于点M,

∵E为BC的中点,∴BE=CE,
∵AB∥CD,∴∠BAE=∠M,
∵∠AEB=∠MEC,∴△ABE≌△MCE,
∴AB=MC,
∵∠BAE=∠EAF,∴∠EAF=∠M.
∴MF=AF,
∵MC=MF+CF,∴AB=AF+FC.
点评:本题主要考查了相似三角形的判定和性质,等腰三角形的性质的知识点.题中作图的理论依据是全等三角形的判定中的边角边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


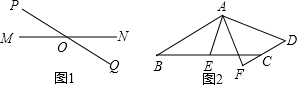 线相交于点F.试探究线段AB与AF、
线相交于点F.试探究线段AB与AF、