题目内容
若一个三角形的两边长分别为2和6,第三边是方程x2－10x＋21＝0的解,则第三边的长为 ( )
| A．7 | B．3 | C．7或3 | D．无法确定 |
A．
试题分析:x2﹣10x+21=0,
因式分解得:（x﹣3）（x﹣7）=0,
解得:x1=3,x2=7,
∵三角形的第三边是x2﹣10x+21=0的解,
∴三角形的第三边为3或7,
当三角形第三边为3时,2+3＜6,不能构成三角形,舍去;
当三角形第三边为7时,三角形三边分别为2,6,7,能构成三角形,
则第三边的长为7．
故选A．
考点:解一元二次方程．
练习册系列答案
学习实践园地系列答案
相关题目
米，则可列方程为（ ）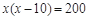
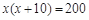
的根是
，x2=6
的解是