Question

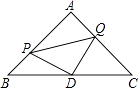
【题目】如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，AB=AC=2，O为AC中点，若点D在直线BC上运动，连接OE，则在点D运动过程中，线段OE的最小值是为（ ）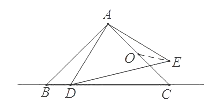

A.
B.
C.1
D.

Answer 1

【答案】B
【解析】设Q是AB的中点，连接DQ，

∵∠BAC=∠DAE=90°，

∴∠BAC-∠DAC=∠DAE-∠DAC，

即∠BAD=∠CAE，

∵AB=AC=2，O为AC中点，

∴AQ=AO，

在△AQD和△AOE中，

，

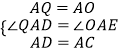∴△AQD≌△AOE（SAS），

∴QD=OE，

∵点D在直线BC上运动，

∴当QD⊥BC时，QD最小，

∵△ABC是等腰直角三角形，

∴∠B=45°，

∵QD⊥BC，

∴△QBD是等腰直角三角形，

∴QD= QB，

∵QB= AB=1，

∴QD= ，

∴线段OE的最小值是为 ．

所以答案是：B．

【考点精析】本题主要考查了垂线段最短和等腰三角形的性质的相关知识点，需要掌握连接直线外一点与直线上各点的所有线段中，垂线段最短；现实生活中开沟引水，牵牛喝水都是“垂线段最短”性质的应用；等腰三角形的两个底角相等（简称：等边对等角）才能正确解答此题．