题目内容
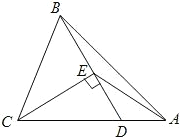
在△ABC中,D为BC边的中点,E为AC边上的任意一点,BE交AD于点O.某学生在研究这一问题时,发现了如下的事实:
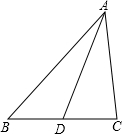
(1)当
| AE |
| AC |
| 1 |
| 2 |
| 1 |
| 1+1 |
| AO |
| AD |
| 2 |
| 3 |
| 2 |
| 2+1 |
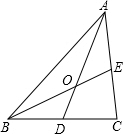
(2)当
| AE |
| AC |
| 1 |
| 3 |
| 1 |
| 1+2 |
| AO |
| AD |
| 2 |
| 4 |
| 2 |
| 2+2 |
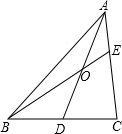
(3)当
| AE |
| AC |
| 1 |
| 4 |
| 1 |
| 1+3 |
| AO |
| AD |
| 2 |
| 5 |
| 2 |
| 2+3 |
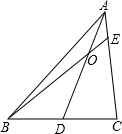
在图中,当
| AE |
| AC |
| 1 |
| 1+n |
| AO |
| AD |
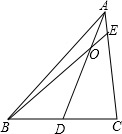
分析:过D作DF∥BE,即求AE:AD,因为
=
,可以根据平行线分线段成比例,及线段相互间的关系即可得出.
| AE |
| AC |
| 1 |
| 1+n |
解答:解:过D作DF∥BE,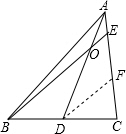
∴AO:AD=AE:AF.
∵D为BC边的中点,
∴CF=EF=0.5EC.
∵
=
,
∴AE:(AE+2EF)=1:(1+n),
AE+2EF=AE+AEn
AEn=2EF,
∴AE:EF=2:n.
∴AE:AF=2:(n+2).
∴
=2:(n+2).

∴AO:AD=AE:AF.
∵D为BC边的中点,
∴CF=EF=0.5EC.
∵
| AE |
| AC |
| 1 |
| 1+n |
∴AE:(AE+2EF)=1:(1+n),
AE+2EF=AE+AEn
AEn=2EF,
∴AE:EF=2:n.
∴AE:AF=2:(n+2).
∴
| AO |
| AD |
点评:本题考查平行线分线段定理及其应用,注意D为BC边的中点的运用.

练习册系列答案
相关题目
 已知:如图,在△ABC中,AD为BC边上的高,∠B=45°,∠C=30°,AD=2.求△ABC的面积.
已知:如图,在△ABC中,AD为BC边上的高,∠B=45°,∠C=30°,AD=2.求△ABC的面积.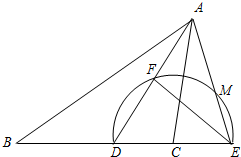 AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.
AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.
 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是76cm2,AB=20cm,AC=18cm,求DE的长.
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是76cm2,AB=20cm,AC=18cm,求DE的长.