题目内容
关于x的方程x2 +mx +m-1=0的两个实数根为x1、x2，且x12+x22=5，求实数m的值.
由题意，得x1 +x2 =-m，x1x2 =m-1.
∵x12 +x22 =(x1 +x2)2-2x1x2=5，
∴(-m)2-2(m-1)=5.解得，m1=3，m2=-1.
∵⊿=m2-4(m-1)=(m-2)2≥0，
∴m=3或-1.
∵x12 +x22 =(x1 +x2)2-2x1x2=5，
∴(-m)2-2(m-1)=5.解得，m1=3，m2=-1.
∵⊿=m2-4(m-1)=(m-2)2≥0，
∴m=3或-1.
欲求m的值，根据x12+x22=5即x12+x22=（x1+x2）2-2x1x2=5，根据一元二次方程根与系数的关系，可以求得两根之积和两根之和，即可得到一个关于m的方程，解方程即可求m的值.
练习册系列答案
相关题目
x2+
x+c－
的解是x1=－2，x2=1（a，m，b均为常数，a≠0），则方程
的解是 。
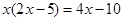
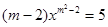是一元二次方程，则
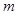的值是（ ）