题目内容
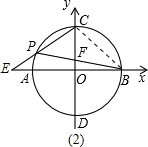
如图1,以点O为圆心,半径为4的圆交x轴于A,B两点,交y轴于C,D两点,点P为弧AC上的一动点,延长CP交x轴于点E;连接PB,交OC于点F.
(1)若点F为OC的中点,求PB的长;
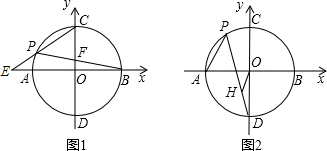
(2)求CP•CE的值;
(3)如图2,过点OH∥AP交PD于点H,当点P在弧AC上运动时,试问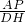 的值是否保持不变;若不变,试证明,求出它的值;若发生变化,请说明理由.
的值是否保持不变;若不变,试证明,求出它的值;若发生变化,请说明理由.
(本题满分8分)
解:(1)连接AP,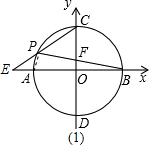
∵AB为⊙O的直径,
∴∠APB=∠FOB=90°.
∵∠ABP=∠FBO,
∴△ABP∽△BOF.
∴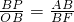 .
.
∵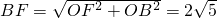 ,
,
∴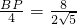 .
.
∴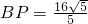 .
.
(2)连接BC,
∵OC⊥AB,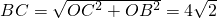 ,
,
∴ =
= ,
,
∴∠CPB=∠EBC.
∵∠BCP=∠BCE,
∴△BCP∽△ECB.
∴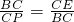 .
.
∴BC2=CP•CE=32.
(3)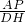 的值保持不变.
的值保持不变.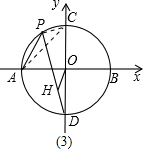
连接PC,AC,
∵OH∥AP,
∴∠APD=∠OHP= ∠AOD=45°.
∠AOD=45°.
∴∠CPA=∠OHD=135°.
又∵∠CAP=∠ODH,
∴△CAP∽△ODH.
∴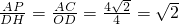 .
.
当点P在弧AC上运动时,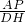 的值保持不变,
的值保持不变,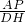 的值为
的值为 .
.
分析:(1)求PB的长,连接AP,可以通过证明△ABP∽△BOF,根据相似三角形的性质得出;
(2)求CP•CE的值,连接BC,CA,易证明AC=BC,得出∠CPB=∠EBC,再证明△BCP∽△ECB,得出比例的乘积形式即可;(3)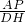 的值可以通过比例的形式,证明△CAP∽△ODH得出.
的值可以通过比例的形式,证明△CAP∽△ODH得出.
点评:本题考查了相似三角形的性质,同时考查了平行线的性质,圆周角的性质,综合性较强.
解:(1)连接AP,

∵AB为⊙O的直径,
∴∠APB=∠FOB=90°.
∵∠ABP=∠FBO,
∴△ABP∽△BOF.
∴
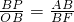 .
.∵
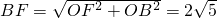 ,
,∴
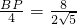 .
.∴
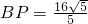 .
.(2)连接BC,
∵OC⊥AB,
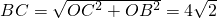 ,
,
∴
 =
= ,
,∴∠CPB=∠EBC.
∵∠BCP=∠BCE,
∴△BCP∽△ECB.
∴
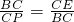 .
.∴BC2=CP•CE=32.
(3)
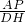 的值保持不变.
的值保持不变.
连接PC,AC,
∵OH∥AP,
∴∠APD=∠OHP=
 ∠AOD=45°.
∠AOD=45°.∴∠CPA=∠OHD=135°.
又∵∠CAP=∠ODH,
∴△CAP∽△ODH.
∴
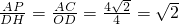 .
.当点P在弧AC上运动时,
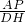 的值保持不变,
的值保持不变,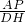 的值为
的值为 .
.分析:(1)求PB的长,连接AP,可以通过证明△ABP∽△BOF,根据相似三角形的性质得出;
(2)求CP•CE的值,连接BC,CA,易证明AC=BC,得出∠CPB=∠EBC,再证明△BCP∽△ECB,得出比例的乘积形式即可;(3)
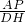 的值可以通过比例的形式,证明△CAP∽△ODH得出.
的值可以通过比例的形式,证明△CAP∽△ODH得出.点评:本题考查了相似三角形的性质,同时考查了平行线的性质,圆周角的性质,综合性较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 23、如图,在以点O为圆心的两个同心圆中,小圆直径AE的延长线与大圆交于点B,点D在大圆上,BD与小圆相切于点F,AF的延长线与大圆相交于点C,且CE⊥BD.找出图中相等的线段并证明.
23、如图,在以点O为圆心的两个同心圆中,小圆直径AE的延长线与大圆交于点B,点D在大圆上,BD与小圆相切于点F,AF的延长线与大圆相交于点C,且CE⊥BD.找出图中相等的线段并证明.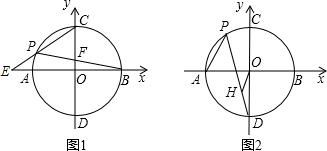

 22、如图,在以点O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于A,与大圆相交于点B,小圆的切线AC与大圆相交于D,OC平分∠ACB.
22、如图,在以点O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于A,与大圆相交于点B,小圆的切线AC与大圆相交于D,OC平分∠ACB.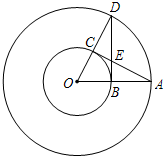 (2006•上海模拟)已知:如图,在以点O为圆心的两个同心圆中,大圆的半径OA与小圆相交于点B,AC与小圆相切于点C,OC的延长线与大圆相交于点D,AC与BD相交于点E.
(2006•上海模拟)已知:如图,在以点O为圆心的两个同心圆中,大圆的半径OA与小圆相交于点B,AC与小圆相切于点C,OC的延长线与大圆相交于点D,AC与BD相交于点E.