题目内容
一天,小明在做剪纸拼图游戏时,无意中,他把如图所示的一张正三角形纸片和一张扇形纸片叠在一起,且正三角形的中心O恰好为扇形的圆心,接着,他把扇形绕点O转动,….
(1)小明思考这样一个问题:在把扇形绕点O转动时,两张纸片的重叠部分面积是否一定会保持不变呢?你能帮助小明解答这一问题吗?你若认为重叠部分面积能保持不变,请说明理由;若认为不能保持不变,请问对这两张纸片再增加什么条件,就能使得扇形绕点O转动过程中它们的重叠部分面积一定会保持不变?请说明理由.
(2)由这一游戏,你还能联想到怎样的图形在变换过程中,也具有类似的性质?请画出图形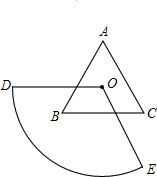 ,并作简要阐述,不要求证明.
,并作简要阐述,不要求证明.
解:(1)两张纸片的重叠部分面积不一定会保持不变.应增加条件“扇形纸片的圆心角∠DOE为120°”
简证如下:连接OB、OC,因为点O是等边△ABC的中心,所以OB、OC为角平分线,且OB=OC,可证△OGB≌△OFC,从而重叠部分面积等于△OBC的面积,即等于等边△ABC的面积的 (定值).
(定值).


(2)由这一游戏,还能联想到如图所示的两个正方形:点O为正方形ABCD的对称中心,另一正方形OEFG绕点O旋转过程中,两个正方形的重叠部分面积保持不变,总是正方形ABCD的面积的 .
.
分析:(1)因为重叠部分总等于三角形面积的 ,可以先从三角形考虑,O为中心也就是与正三角形的中心角重合,所以应为120°,证明是要分两种情况:即特殊和一般,特殊情况时就是猜想所用的情况,显然成立,一般情况的证明从三角形全等把四边形的面积分解成两个三角形,最后再归到正三角形的中心角为120°的三角形.
,可以先从三角形考虑,O为中心也就是与正三角形的中心角重合,所以应为120°,证明是要分两种情况:即特殊和一般,特殊情况时就是猜想所用的情况,显然成立,一般情况的证明从三角形全等把四边形的面积分解成两个三角形,最后再归到正三角形的中心角为120°的三角形.
(2)利用相同的作法还可以得到点O为正方形ABCD的对称中心,另一正方形OEFG绕点O旋转过程中,两个正方形的重叠部分面积保持不变,总是正方形ABCD的面积的 .
.
点评:本题考查了全等三角形的判定与性质及等边三角形的性质;猜想时从三角形考虑是解答本题的突破点,证明时一般情况的证明容易被学生忽视.
简证如下:连接OB、OC,因为点O是等边△ABC的中心,所以OB、OC为角平分线,且OB=OC,可证△OGB≌△OFC,从而重叠部分面积等于△OBC的面积,即等于等边△ABC的面积的
 (定值).
(定值).

(2)由这一游戏,还能联想到如图所示的两个正方形:点O为正方形ABCD的对称中心,另一正方形OEFG绕点O旋转过程中,两个正方形的重叠部分面积保持不变,总是正方形ABCD的面积的
 .
.分析:(1)因为重叠部分总等于三角形面积的
 ,可以先从三角形考虑,O为中心也就是与正三角形的中心角重合,所以应为120°,证明是要分两种情况:即特殊和一般,特殊情况时就是猜想所用的情况,显然成立,一般情况的证明从三角形全等把四边形的面积分解成两个三角形,最后再归到正三角形的中心角为120°的三角形.
,可以先从三角形考虑,O为中心也就是与正三角形的中心角重合,所以应为120°,证明是要分两种情况:即特殊和一般,特殊情况时就是猜想所用的情况,显然成立,一般情况的证明从三角形全等把四边形的面积分解成两个三角形,最后再归到正三角形的中心角为120°的三角形.(2)利用相同的作法还可以得到点O为正方形ABCD的对称中心,另一正方形OEFG绕点O旋转过程中,两个正方形的重叠部分面积保持不变,总是正方形ABCD的面积的
 .
.点评:本题考查了全等三角形的判定与性质及等边三角形的性质;猜想时从三角形考虑是解答本题的突破点,证明时一般情况的证明容易被学生忽视.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
将所有正奇数按下表排列:
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 |
| 1 | 3 | 5 | 7 | |
| 15 | 13 | 11 | 9 | |
| 17 | 19 | 21 | 23 | |
| 31 | 29 | 27 | 25 | |
| 33 | … | … | … |
- A.251行4列
- B.250行2列
- C.250行3列
- D.251行2列
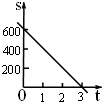

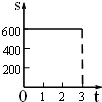
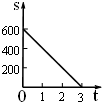
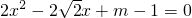 有实数根,则直线l与⊙O的位置关系为
有实数根,则直线l与⊙O的位置关系为 如图,AB=CD,DE=AF,CF=BE,∠AFB=80°,∠CDE=60°,那么∠ABC等于
如图,AB=CD,DE=AF,CF=BE,∠AFB=80°,∠CDE=60°,那么∠ABC等于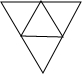 如图是一个等边三角形连接各边中点形成的图形,则它是下列哪种几何体的平面展开图
如图是一个等边三角形连接各边中点形成的图形,则它是下列哪种几何体的平面展开图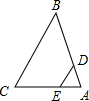 如图,在△ABC中,已知DE∥BC,且AE=1,AC=4,DE=
如图,在△ABC中,已知DE∥BC,且AE=1,AC=4,DE= ,则BC的长为
,则BC的长为