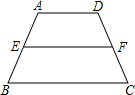
题目内容
 如果连接梯形两腰的中点,把这条线段叫做梯形的中位线,那么梯形的中位线有什么特征呢?
如果连接梯形两腰的中点,把这条线段叫做梯形的中位线,那么梯形的中位线有什么特征呢?如图,梯形ABCD中,AD∥BC、点E、F分别为两腰AB、CD的中点.
猜想:EF=
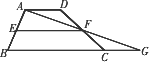
分析:连接AF并延长交BC的延长线于G,则△ADF≌△GCF,则△ABG的面积等于梯形ABCD的面积,EF是△ABG的中位线,即可证明.
解答: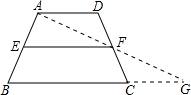 解:连接AF并延长交BC的延长线于G,
解:连接AF并延长交BC的延长线于G,
∵AD∥BC,
∴∠DAF=∠CGF,
在△ADF与△GCF中
∴△ADF≌△GCF,
∴AD=CG
∵EF是△ABG的中位线,
∴EF=
BG=
(BC+CG),
∴EF=
(BC+AD),
故答案为:
(BC+AD).
 解:连接AF并延长交BC的延长线于G,
解:连接AF并延长交BC的延长线于G,∵AD∥BC,
∴∠DAF=∠CGF,
在△ADF与△GCF中
|
∴△ADF≌△GCF,
∴AD=CG
∵EF是△ABG的中位线,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴EF=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:此题考查梯形中位线的证明方法,辅助线的作法要记住.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
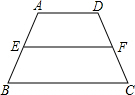 如果连接梯形两腰的中点,把这条线段叫做梯形的中位线,那么梯形的中位线有什么特征呢?
如果连接梯形两腰的中点,把这条线段叫做梯形的中位线,那么梯形的中位线有什么特征呢?