题目内容
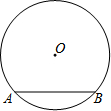（2013•南京二模）如图，⊙O的直径为10，弦AB的长为8，则点O到AB的距离为3
3
．分析：首先过点O作OC⊥AB于点C，连接OA，由垂径定理即可求得AC的长，然后勾股定理求得答案．
解答：
解：过点O作OC⊥AB于点C，连接OA，
∴AC=
AB=
×8=4，
∵⊙O的直径为10，
∴OA=5，
∴在Rt△OAC中，OC=
=3．
即点O到AB的距离为3．
故答案为：3．
解：过点O作OC⊥AB于点C，连接OA，∴AC=
| 1 |
| 2 |
| 1 |
| 2 |
∵⊙O的直径为10，
∴OA=5，
∴在Rt△OAC中，OC=
| OA2-AC2 |
即点O到AB的距离为3．
故答案为：3．
点评：此题考查了垂径定理与勾股定理．此题比较简单，注意掌握辅助线的作法，注意数形结合思想的应用．
练习册系列答案
相关题目
