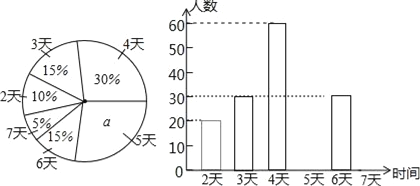
��Ŀ����
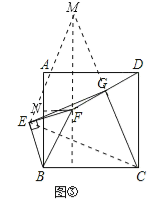
����Ŀ����֪������ABCD�У�EΪ�Խ���BD��һ�㣬��E����EF��BD��BC��F������DF��GΪDF�е㣬����EG��CG��

��1����֤��EG=CG��
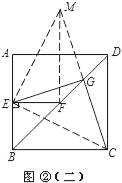
��2����ͼ������BEF��B����ʱ����ת45������ͼ����ʾ��ȡDF�е�G������EG��CG��
�ʣ�1���еĽ����Ƿ���Ȼ�������������������֤����������������˵�����ɣ�
��3����ͼ������BEF��B����ת����Ƕȣ���ͼ����ʾ����������Ӧ���߶Σ��ʣ�1���еĽ����Ƿ���Ȼ������ͨ���۲��㻹�ܵó�ʲô���ۣ�����Ҫ��֤������
���𰸡��������.
�������������������1������ֱ��������б���ϵ����ߵ���б�ߵ�һ�룬��֤��CG=EG��
��2��������Ȼ����������AG����G����MN��AD��M����EF���ӳ��߽���N�㣻��֤����DAG�ա�DCG���ó�AG=CG����֤����DMG�ա�FNG���õ�MG=NG����֤����AMG�ա�ENG���ó�AG=EG�����֤��CG=EG��
��3��������Ȼ��������֪��EG��CG��
��1��֤�������ı���ABCD�������Σ�
���DCF=90����
��Rt��FCD��
��GΪDF���е㣬
��CG=FD��
ͬ������Rt��DEF�У�
EG=FD��
��CG=EG��
��2���⣺��1���н�����Ȼ��������EG=CG��
֤��һ������AG����G����MN��AD��M����EF���ӳ��߽���N�㣮
����DAG����DCG��
��AD=CD����ADG=��CDG��DG=DG��
���DAG�ա�DCG��SAS����
��AG=CG��
����DMG����FNG��
�ߡ�DGM=��FGN��FG=DG����MDG=��NFG��
���DMG�ա�FNG��ASA����
��MG=NG��
�ߡ�EAM=��AEN=��AMN=90����
���ı���AENM�Ǿ��Σ�
�ھ���AENM�У�AM=EN��
����AMG����ENG��
��AM=EN����AMG=��ENG��MG=NG��
���AMG�ա�ENG��SAS����
��AG=EG��
��EG=CG��
֤�������ӳ�CG��M��ʹMG=CG��
����MF��ME��EC��
����DCG����FMG��
��FG=DG����MGF=��CGD��MG=CG��
���DCG�ա�FMG��
��MF=CD����FMG=��DCG��
��MF��CD��AB��
��EF��MF��
��Rt��MFE��Rt��CBE��
��MF=CB����MFE=��EBC��EF=BE��
���MFE�ա�CBE
���MEF=��CEB��
���MEC=��MEF+��FEC=��CEB+��CEF=90����
���MECΪֱ�������Σ�
��MG=CG��
��EG=MC��
��EG=CG��
��3���⣺��1���еĽ�����Ȼ�������������£�
��F��CD��ƽ���߲��ӳ�CG����M�㣬����EM��EC����F��FN��ֱ��AB��N��
����GΪFD�е㣬��֤��CDG�ա�MFG���õ�CD=FM��
����ΪBE=EF����֤��EFM=��EBC������EFM�ա�EBC����FEM=��BEC��EM=EC
�ߡ�FEC+��BEC=90�������FEC+��FEM=90��������MEC=90����
���MEC�ǵ���ֱ�������Σ�
��GΪCM�е㣬
��EG=CG��EG��CG��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�