题目内容
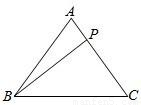
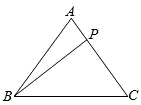 如图,△ABC中,有一点P在AC上移动.若AB=AC=5,BC=6,则AP+BP+CP的最小值为
如图,△ABC中,有一点P在AC上移动.若AB=AC=5,BC=6,则AP+BP+CP的最小值为
- A.8
- B.8.8
- C.9.8
- D.10
C
分析:若AP+BP+CP最小,就是说当BP最小时,AP+BP+CP才最小,因为不论点P在AC上的那一点,AP+CP都等于AC.那么就需从B向AC作垂线段,交AC于P.先设AP=x,再利用勾股定理可得关于x的方程,解即可求x,在Rt△ABP中,利用勾股定理可求BP.那么AP+BP+CP的最小值可求.
解答: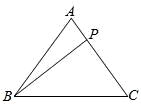 解:从B向AC作垂线段BP,交AC于P,
解:从B向AC作垂线段BP,交AC于P,
设AP=x,则CP=5-x,
在Rt△ABP中,BP2=AB2-AP2,
在Rt△BCP中,BP2=BC2-CP2,
∴AB2-AP2=BC2-CP2,
∴52-x2=62-(5-x)2
解得x=1.4,
在Rt△ABP中,BP= =
=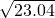 =4.8,
=4.8,
∴AP+BP+CP=AC+BP=5+4.8=9.8.
故选C.
点评:直线外一点与直线上各点连接的所有线段中,垂线段最短.因此先从B向AC作垂线段BP,交AB于P,再利用勾股定理解题即可.
分析:若AP+BP+CP最小,就是说当BP最小时,AP+BP+CP才最小,因为不论点P在AC上的那一点,AP+CP都等于AC.那么就需从B向AC作垂线段,交AC于P.先设AP=x,再利用勾股定理可得关于x的方程,解即可求x,在Rt△ABP中,利用勾股定理可求BP.那么AP+BP+CP的最小值可求.
解答:
 解:从B向AC作垂线段BP,交AC于P,
解:从B向AC作垂线段BP,交AC于P,设AP=x,则CP=5-x,
在Rt△ABP中,BP2=AB2-AP2,
在Rt△BCP中,BP2=BC2-CP2,
∴AB2-AP2=BC2-CP2,
∴52-x2=62-(5-x)2
解得x=1.4,
在Rt△ABP中,BP=
 =
=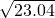 =4.8,
=4.8,∴AP+BP+CP=AC+BP=5+4.8=9.8.
故选C.
点评:直线外一点与直线上各点连接的所有线段中,垂线段最短.因此先从B向AC作垂线段BP,交AB于P,再利用勾股定理解题即可.

练习册系列答案
相关题目
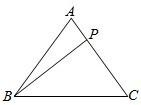 如图,△ABC中,有一点P在AC上移动.若AB=AC=5,BC=6,则AP+BP+CP的最小值为( )
如图,△ABC中,有一点P在AC上移动.若AB=AC=5,BC=6,则AP+BP+CP的最小值为( )| A、8 | B、8.8 | C、9.8 | D、10 |
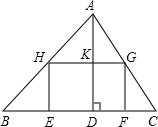 与HG交于K,设GF为x,HG为y.
与HG交于K,设GF为x,HG为y. ,那么
,那么 )
)