题目内容
P点为抛物线 (
( 为常数,
为常数, )上任一点,将抛物线绕顶点
)上任一点,将抛物线绕顶点 逆时针旋转
逆时针旋转 后得到的新图象与
后得到的新图象与 轴交于
轴交于 、
、 两点(点
两点(点 在点
在点 的上方),点
的上方),点 为点
为点 旋转后的对应点.
旋转后的对应点.
1.(1)当 ,点
,点 横坐标为4时,求
横坐标为4时,求 点的坐标;
点的坐标;
2.(2)设点 ,用含
,用含 、
、 的代数式表示
的代数式表示 ;
;
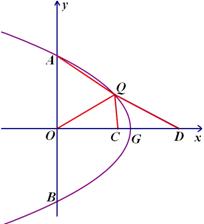
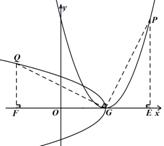
3.(3) 如图,点 在第一象限内, 点
在第一象限内, 点 在
在 轴的正半轴上,点
轴的正半轴上,点 为
为 的中点,
的中点, 平分
平分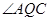 ,
, ,当
,当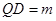 时,求
时,求 的值.
的值.
【答案】
1.(1)当m=2时, ,则
,则 ,
, .
--------------------1分
.
--------------------1分
如图,连接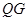 、
、 ,过点
,过点 作
作 轴于
轴于 ,过点
,过点 作
作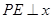 轴于
轴于 .
.
依题意,可得△ ≌△
≌△ .
.
则 ∴
∴  .∴
.∴
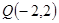 .
.
2.(2)用含 的代数式表示
的代数式表示 :
: .
.
3.(3)如图,延长 到点E,使
到点E,使 ,连接
,连接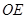 .
.
 ∵
∵  为
为 中点,∴
中点,∴  .
.
∵  ,∴ △
,∴ △ ≌△
≌△ .
.
∴  . ------------------7分
. ------------------7分
∵  ,∴
,∴  .
.
∵  平分
平分 ,∴
,∴
 .
.
∴ △ ≌△
≌△ .
------------------9分
.
------------------9分
∴  .∴
.∴ 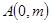 .-----------------10分
.-----------------10分
∵ 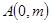 在新的图象上, ∴
在新的图象上, ∴  .
.
∴  ,
, (舍).∴
(舍).∴  .
------------------12分
.
------------------12分

【解析】略

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
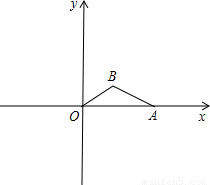
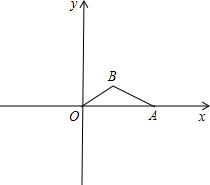 如图,在平面直角坐标系xOy中,△OAB的顶点A的坐标为(10,0),顶点B在第一象限内,且|AB|=3
如图,在平面直角坐标系xOy中,△OAB的顶点A的坐标为(10,0),顶点B在第一象限内,且|AB|=3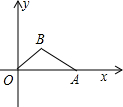 如图,在平面直角坐标系xOy中,△OAB的顶点A的坐标为(10,0),顶点B在第一象限内,且
如图,在平面直角坐标系xOy中,△OAB的顶点A的坐标为(10,0),顶点B在第一象限内,且
 ,sin∠OAB=
,sin∠OAB=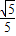 .
.
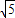 ,sin∠OAB=
,sin∠OAB= .
.