题目内容
如图,乒乓球的最大截口⊙O的直径AB垂直于弦CD,P为垂足,若CD=32cm,AP:PB=1:4,则AB= .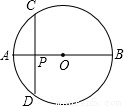
【答案】分析:首先连接OC,由AP:PB=1:4,可设AP=xcm,PB=4xcm,即可求得OC与OP的值,又由垂径定理求得PC的长,然后由CD=32cm,可得方程,解方程即可求得AB的长.
解答: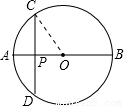 解:连接OC,
解:连接OC,
∵AP:PB=1:4,
设AP=xcm,PB=4xcm,
则AB=5x,OA=OC= xcm,
xcm,
∴OP=OA-PA= xcm,
xcm,
∵AB⊥CD,
∴PC= CD=
CD= ×32=16(cm),
×32=16(cm),
在Rt△OPC中,PC=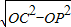 =2xcm,
=2xcm,
∴2x=16,
∴x=8,
∴AB=5x=40(cm).
故答案为:40.
点评:此题考查了垂径定理与勾股定理的应用.此题难度不大,解题的关键是注意数形结合思想与方程思想的应用,注意辅助线的作法.
解答:
 解:连接OC,
解:连接OC,∵AP:PB=1:4,
设AP=xcm,PB=4xcm,
则AB=5x,OA=OC=
 xcm,
xcm,∴OP=OA-PA=
 xcm,
xcm,∵AB⊥CD,
∴PC=
 CD=
CD= ×32=16(cm),
×32=16(cm),在Rt△OPC中,PC=
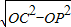 =2xcm,
=2xcm,∴2x=16,
∴x=8,
∴AB=5x=40(cm).
故答案为:40.
点评:此题考查了垂径定理与勾股定理的应用.此题难度不大,解题的关键是注意数形结合思想与方程思想的应用,注意辅助线的作法.

练习册系列答案
相关题目
 如图,乒乓球的最大截口⊙O的直径AB垂直于弦CD,P为垂足,若CD=32cm,AP:PB=1:4,则AB=
如图,乒乓球的最大截口⊙O的直径AB垂直于弦CD,P为垂足,若CD=32cm,AP:PB=1:4,则AB=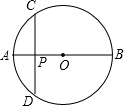 如图,乒乓球的最大截口⊙O的直径AB垂直于弦CD,P为垂足,若CD=32cm,AP:PB=1:4,则AB=________.
如图,乒乓球的最大截口⊙O的直径AB垂直于弦CD,P为垂足,若CD=32cm,AP:PB=1:4,则AB=________.