题目内容
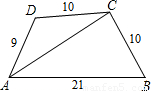
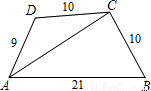
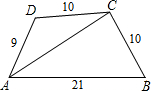As in right figure，in a quadrilateral ABCD，we have its diagonal AC bisects∠DAB，and AB=21，AD=9，BC=DC=10，then the distance from point C to line AB is分析：作辅助线构建直角三角形，求证△CED≌△CFB，即可得DE=FB，即可求得BF，根据BF求CF，根据CF、AF求AC．
解答：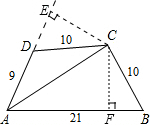
解：过C作CE⊥AD，CF⊥AB，
∴△CED≌△CFB，
∴DE=FB，
∴9+DE=21-BF，
∴BF=6，
根据勾股定理，可知CF=CE=8，即点C到AB的距离为8．
∴AC=
=
=17．
故答案为：8，17．
解：过C作CE⊥AD，CF⊥AB，∴△CED≌△CFB，
∴DE=FB，
∴9+DE=21-BF，
∴BF=6，
根据勾股定理，可知CF=CE=8，即点C到AB的距离为8．
∴AC=
| AF2+CF2 |
| 152+82 |
故答案为：8，17．
点评：本题考查了角平分线的性质及全等三角形的证明，勾股定理在直角三角形中的应用，解答本题构建直角△CFD是关键．
练习册系列答案
相关题目
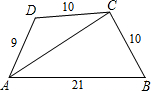As in right figure，in a quadrilateral ABCD，we have its diagonal AC bisects∠DAB，and AB=21，AD=9，BC=DC=10，then the distance from point C to line AB is________，and the length of AC is________． （英汉词典：quadrilateral 四边形；bisect 平分）
