题目内容
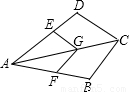
阅读下列短文:如图,G是四边形ABCD对角线AC上一点,过G作GE∥CD交AD于E,GF∥CB交AB于F,若EG=FG,则有BC=CD成立,同时可知四边形ABCD与四边形AFGE相似.
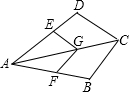
解答问题:
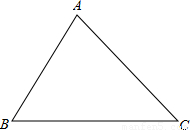
(1)有一块三角形空地(如图△ABC),BC邻近公路,现需在此空地上修建一个正方形广场,其余地为草坪,要使广场一边靠公路,且其面积最大,如何设计,请你在下面图中画出此广场正方形.(尺规作图,不写作法)
(2)锐角△ABC是一块三角形余料,边AB=130mm,BC=150mm,AC=140mm,要把它加工成正方形零件,使正方形的一边在三角形的一边上,其余两个顶点分别在另外两条边上,且剪去正方形零件后剩下的边角料较少,这个正方形零件的边长是多少?你能得出什么结论,并证明你的结论.
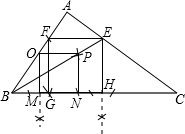
分析:(1)先在AB上任取一点O,过O作BC的垂线,然后作出以OM为一边的正方形OMNP,连接BP并延长交AC于点E,过点E作BC的垂线交BC于点H,再以EH为边作正方形EFGH即可;
(2)过A作AD⊥BC于点D,在Rt△ABD与Rt△ACD中,根据AD是公共边利用勾股定理列式求出BD的长,再利用勾股定理求出AD的长,然后利用△ABC的面积求出AB、AC边上的高,设正方形的边长为a,根据相似三角形对应高的比等于对应边的比列出比例式求解得到正方形的边长与三角形的边与相应边上的高的关系,然后判断出当边与边上的高的和最小时,正方形的边长最大,剪去正方形零件后剩下的边角料较少,然后计算即可得解.
(2)过A作AD⊥BC于点D,在Rt△ABD与Rt△ACD中,根据AD是公共边利用勾股定理列式求出BD的长,再利用勾股定理求出AD的长,然后利用△ABC的面积求出AB、AC边上的高,设正方形的边长为a,根据相似三角形对应高的比等于对应边的比列出比例式求解得到正方形的边长与三角形的边与相应边上的高的关系,然后判断出当边与边上的高的和最小时,正方形的边长最大,剪去正方形零件后剩下的边角料较少,然后计算即可得解.
解答:解:(1)如图;
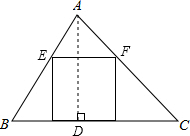
(2)如图,过A作AD⊥BC于点D,则CD=BC-BD=150-BD,
在Rt△ABD中,AD2=AB2-BD2=1302-BD2,
在Rt△ACD中,AD2=AC2-CD2=1402-(150-BD)2,
所以,1302-BD2=1402-(150-BD)2,
解得BD=
=
=66,
所以,AD2=1302-662=12544,
AD=112mm,
设AB、AC边上的高分别为hAB,hAC,
则S△ABC=
×130×hAB=
×140×hAC=
×150×112,
解得hAB=129
mm,hAC=120mm,
设正方形的边长为a,
∵EF∥BC,
∴△AEF∽△ABC,
∴
=
,
即
=
,
整理得,a=
,
∵BC•AD是△ABC面积的2倍,
∴BC+AD,也就是三角形一条边与这条边上的高的和越小,则加工成的正方形的边长越大,面积也就是越大,剪去正方形零件后剩下的边角料较少,
130+129
=259
mm,
140+120=260mm,
150+112=262mm,
∵259
<260<262,
∴有两个顶点在AB=130mm边上加工成的正方形的面积最大,
这个正方形的边长为
=
=64
mm.
结论:正方形的一条边在三角形的哪一条边上,则正方形的边长等于这条边与这条边上的高的积除以它们的和,并且最短边上的正方形的边长最大.

(2)如图,过A作AD⊥BC于点D,则CD=BC-BD=150-BD,

在Rt△ABD中,AD2=AB2-BD2=1302-BD2,
在Rt△ACD中,AD2=AC2-CD2=1402-(150-BD)2,
所以,1302-BD2=1402-(150-BD)2,
解得BD=
| 1302+1502-1402 |
| 2×150 |
| 19800 |
| 300 |
所以,AD2=1302-662=12544,
AD=112mm,
设AB、AC边上的高分别为hAB,hAC,
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得hAB=129
| 3 |
| 13 |
设正方形的边长为a,
∵EF∥BC,
∴△AEF∽△ABC,
∴
| EF |
| BC |
| AD-a |
| AD |
即
| a |
| BC |
| AD-a |
| AD |
整理得,a=
| BC•AD |
| BC+AD |
∵BC•AD是△ABC面积的2倍,
∴BC+AD,也就是三角形一条边与这条边上的高的和越小,则加工成的正方形的边长越大,面积也就是越大,剪去正方形零件后剩下的边角料较少,
130+129
| 3 |
| 13 |
| 3 |
| 13 |
140+120=260mm,
150+112=262mm,
∵259
| 3 |
| 13 |
∴有两个顶点在AB=130mm边上加工成的正方形的面积最大,
这个正方形的边长为
130×129
| ||
130+129
|
| 21840 |
| 3370 |
| 272 |
| 337 |
结论:正方形的一条边在三角形的哪一条边上,则正方形的边长等于这条边与这条边上的高的积除以它们的和,并且最短边上的正方形的边长最大.
点评:本题考查了相似三角形的应用,根据相似三角形对应高的比等于对应边的比列式计算是解题的关键,(1)中,读懂题目信息并利用信息是正确作图的关键,对同学们信息获取能力的要求比较高.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目