题目内容
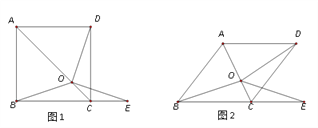
【题目】如图1,在正方形ABCD中,O是对角线AC上一点,点E在BC的延长线上,且OE = OB.
(1)求证:△OBC ≌ △ODC.
(2)求证:∠DOE = ∠ABC.
(3)把正方形ABCD改为菱形,其他条件不变(如图2),若∠ABC = 52° ,求∠DOE的度数.
【答案】(1)证明见解析; (2)证明见解析; (3)52°.
【解析】试题分析:(1)根据正方形的四条边都相等可得BC=DC,对角线平分一组对角可得∠BCO=∠DCO,然后利用“边角边”证明即可;
(2)根据全等三角形对应角相等可得∠CBO=∠CDO,根据等边对等角可得∠CBO=∠E,然后求出∠DOE=∠DCE,再根据两直线平行,同位角相等可得∠DCE=∠ABC,从而得证;
(3)根据(2)的结论解答.
试题解析(1)证明:在正方形ABCD中,BC=DC,∠BCO=∠DCO=45°,
∵在△BCO和△DCO中,
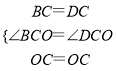 ,
,
∴△BCO≌△DCO(SAS);
(2)由(1)知,△BCO≌△DCO,
∴∠CBO=∠CDO,
∵OE=OB,
∴∠CBO=∠E,
∵∠1=∠2(对顶角相等),
∴180°-∠1-∠CDO=180°-∠2-∠E,
即∠DOE=∠DCE,
∵AB∥CD,
∴∠DCE=∠ABC,
∴∠DOE=∠ABC;
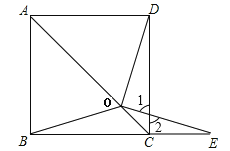
(3)解:与(2)同理可得:∠DOE=∠ABC,
∵∠ABC=52°,
∴∠DPE=52°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目