题目内容
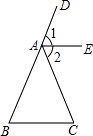 如图,AE平分∠CAD,且AE∥BC,给出下列结论:①∠1=∠B,②∠2=∠C,③∠B=∠C,④2∠B+∠BAE=180°,其中正确的有
如图,AE平分∠CAD,且AE∥BC,给出下列结论:①∠1=∠B,②∠2=∠C,③∠B=∠C,④2∠B+∠BAE=180°,其中正确的有
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:由AE∥BC,根据两直线平行,同位角相等,两直线平行,内错角相等,两直线平行,同旁内角互补,即可判定①②正确,④错误;又由AE平分∠CAD,即可判定③正确,继而求得答案.
解答:∵AE∥BC,
∴∠1=∠B,∠2=∠C,∠B+∠BAE=180°,
故①②正确,④错误;
∵AE平分∠CAD,
∴∠1=∠2,
∴∠B=∠C,
故③正确.
∴其中正确的有①②③.
故选C.
点评:此题考查了平行线的性质与角平分线的定义.此题比较简单,解题的关键是注意掌握两直线平行,同位角相等,两直线平行,内错角相等与两直线平行,同旁内角互补定理的应用,注意数形结合思想的应用.
分析:由AE∥BC,根据两直线平行,同位角相等,两直线平行,内错角相等,两直线平行,同旁内角互补,即可判定①②正确,④错误;又由AE平分∠CAD,即可判定③正确,继而求得答案.
解答:∵AE∥BC,
∴∠1=∠B,∠2=∠C,∠B+∠BAE=180°,
故①②正确,④错误;
∵AE平分∠CAD,
∴∠1=∠2,
∴∠B=∠C,
故③正确.
∴其中正确的有①②③.
故选C.
点评:此题考查了平行线的性质与角平分线的定义.此题比较简单,解题的关键是注意掌握两直线平行,同位角相等,两直线平行,内错角相等与两直线平行,同旁内角互补定理的应用,注意数形结合思想的应用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 58、先作图,再证明.
58、先作图,再证明.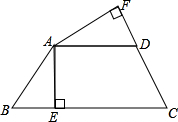 如图,在四边形ABCD中,AB=AD,CA平分∠BCD,AE⊥BC于E,AF⊥CD交CD延长线于F.求证:BE=DF.
如图,在四边形ABCD中,AB=AD,CA平分∠BCD,AE⊥BC于E,AF⊥CD交CD延长线于F.求证:BE=DF.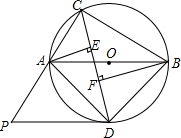 (2013•襄阳)如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
(2013•襄阳)如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F. 如图,等腰直角△ABC中,CA=CB,点E为△ABC外一点,CE=CA,且CD平分∠ACB交AE于D,且∠CDE=60°.
如图,等腰直角△ABC中,CA=CB,点E为△ABC外一点,CE=CA,且CD平分∠ACB交AE于D,且∠CDE=60°.