题目内容
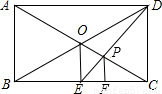
(2004•深圳)在矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BC,垂足为E,连接DE交AC于点P,过P作PF⊥BC,垂足为F,则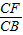 的值是 .
的值是 .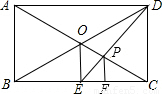
【答案】分析:根据题意易证△OBE∽△DBC和△EPF∽△EDC,利用相似三角形的相似比求解.
解答:解:∵OB=OD= BD,OE⊥BC,CD⊥BC,
BD,OE⊥BC,CD⊥BC,
∴△OBE∽△DBC,
∴OE:CD=1:2,
∵OE∥CD,
∴△OEP∽△CDP,
∴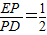 ,
,
∵PF∥DC,
∴△EPF∽△EDC,
∴ ,
,
∵CE= BC,
BC,
∴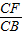 =
= .
.
故答案为 .
.
点评:本题考查对相似三角形性质的理解.相似三角形对应边的比相等.
解答:解:∵OB=OD=
 BD,OE⊥BC,CD⊥BC,
BD,OE⊥BC,CD⊥BC,∴△OBE∽△DBC,
∴OE:CD=1:2,
∵OE∥CD,
∴△OEP∽△CDP,
∴
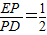 ,
,∵PF∥DC,
∴△EPF∽△EDC,
∴
 ,
,∵CE=
 BC,
BC,∴
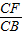 =
= .
.故答案为
 .
.点评:本题考查对相似三角形性质的理解.相似三角形对应边的比相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
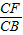 的值是 .
的值是 .