题目内容
已知函数y=ax2+bx+c,当y>0时,-
<x<
.则函数y=cx2-bx+a的图象可能是下图中的( )
| 1 |
| 2 |
| 1 |
| 3 |
A、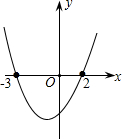 |
B、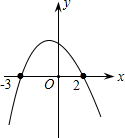 |
C、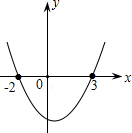 |
D、 |
分析:当y>0时,-
<x<
,所以可判断a<0,可知-
=-
+
=-
,
=-
×
=-
,所以可知a=6b,a=-6c,则b=-c,不妨设c=1进而得出解析式,找出符合要求的答案.
| 1 |
| 2 |
| 1 |
| 3 |
| b |
| a |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| c |
| a |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
解答:解:因为函数y=ax2+bx+c,当y>0时,-
<x<
所以可判断a<0,可知-
=-
+
=-
,
=-
×
=-
所以可知a=6b,a=-6c,则b=-c,不妨设c=1
则函数y=cx2-bx+a为函数y=x2+x-6
即y=(x-2)(x+3)
则可判断与x轴的交点坐标是(2,0),(-3,0),
故选A.
| 1 |
| 2 |
| 1 |
| 3 |
所以可判断a<0,可知-
| b |
| a |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| c |
| a |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
所以可知a=6b,a=-6c,则b=-c,不妨设c=1
则函数y=cx2-bx+a为函数y=x2+x-6
即y=(x-2)(x+3)
则可判断与x轴的交点坐标是(2,0),(-3,0),
故选A.
点评:要考查了从图象上把握有用的条件,准确选择数量关系解得a,b,c的值.从条件可判断出a<0,可知-
=-
,
=-
;所以可知a=-6,b=-1,c=1,从而可判断后一个函数图象.
| b |
| a |
| 1 |
| 6 |
| c |
| a |
| 1 |
| 6 |

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
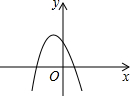
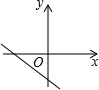
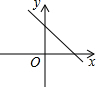
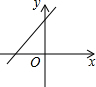
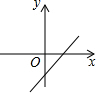
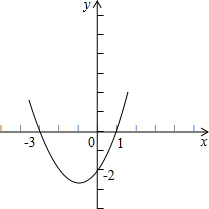 已知函数y=ax2+bx+c的图象如图所示,试根据图象回答下列问题:
已知函数y=ax2+bx+c的图象如图所示,试根据图象回答下列问题: