题目内容
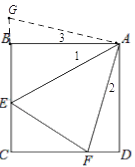
【题目】如图E、F分别在正方形ABCD的边BC、CD上,且∠EAF=45°.
(1)求证:EF=BE+DF;
(2)若线段EF、AB的长分别是方程x2﹣5x+6=0的两个根,求△AEF的面积.

【答案】(1)证明见解析;(2)3
【解析】试题分析:(1)延长CB到G,使GB=DF,连接AG,求证△ABG≌△ADF,得∠3=∠2,AG=AF,进而求证△AGE≌△AFE,可得GB+BE=EF,所以DF+BE=EF;
(2)解方程求得EF、AB的长,由S△AEF=S△AGE ,通过计算即可得.
试题解析:(1)延长CB到G,使GB=DF,连接AG(如图),
∵AB=AD,∠ABG=∠D=90°,GB=DF,∴△ABG≌△ADF(SAS),
∴∠3=∠2,AG=AF,
∵∠BAD=90°,∠EAF=45°,
∴∠1+∠2=45°,∴∠GAE=∠1+∠3=45°=∠EAF,
∵AE=AE,∠GAE=∠EAF,AG=AF,
∴△AGE≌△AFE(SAS),
∴GB+BE=EF,∴EF= BE + DF.
(2)∵x2-5x+6=0,∴x1= 2,x2= 3,
S△AEF=S△AGE=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目