题目内容
点D、E、F分别是△ABC三边中点,且S△DEF=3,则△ABC的面积为
- A.12
- B.9
- C.6
- D.15
A
分析:根据三角形的中位线定理求出两三角形相似并求出它们的相似比,再根据相似三角形的面积的比等于相似比的平方解答.
解答: 解:如图,∵点D、E、F分别是△ABC三边中点,
解:如图,∵点D、E、F分别是△ABC三边中点,
∴DE= BC,EF=
BC,EF= AB,DF=
AB,DF= AC,
AC,
∴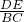 =
=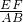 =
=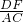 =
= ,
,
∴△DEF∽△ABC,
∵S△DEF=3,
∴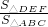 =
= =(
=( )2,
)2,
解得S△ABC=12.
故选A.
点评:本题考查了相似三角形的判定与性质,三角形的中位线定理,根据三角形的中位线定理求出两三角形的三边对应成比例,从而判定出两三角形相似是解题的关键.
分析:根据三角形的中位线定理求出两三角形相似并求出它们的相似比,再根据相似三角形的面积的比等于相似比的平方解答.
解答:
 解:如图,∵点D、E、F分别是△ABC三边中点,
解:如图,∵点D、E、F分别是△ABC三边中点,∴DE=
 BC,EF=
BC,EF= AB,DF=
AB,DF= AC,
AC,∴
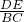 =
=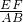 =
=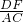 =
= ,
,∴△DEF∽△ABC,
∵S△DEF=3,
∴
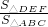 =
= =(
=( )2,
)2,解得S△ABC=12.
故选A.
点评:本题考查了相似三角形的判定与性质,三角形的中位线定理,根据三角形的中位线定理求出两三角形的三边对应成比例,从而判定出两三角形相似是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
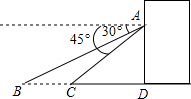 如图,小明家住16楼,楼前有一条河.小明在阳台距离地面50米的A点(AD=50m)分别看向河的两岸(B点和C点),测得俯角分别是45°与30°,请你求出河宽是多少?(精确到0.1米)
如图,小明家住16楼,楼前有一条河.小明在阳台距离地面50米的A点(AD=50m)分别看向河的两岸(B点和C点),测得俯角分别是45°与30°,请你求出河宽是多少?(精确到0.1米)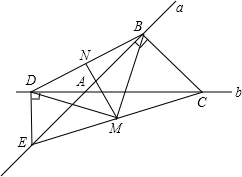 如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是中点.
如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是中点.
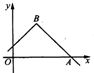 函数y=3-|x-2|的图象如图所示,则点A与B的坐标分别是A(
函数y=3-|x-2|的图象如图所示,则点A与B的坐标分别是A(