题目内容
【题目】如图,已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数y=﹣![]() 的图象与线段AB交于M点,且AM=BM,过点M作MC⊥x轴于点C,MD⊥y轴于点D.
的图象与线段AB交于M点,且AM=BM,过点M作MC⊥x轴于点C,MD⊥y轴于点D.
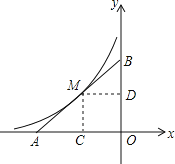
(1)求证:MC=MD;
(2)求点M的坐标;
(3)求直线AB的解析式.
【答案】(1)见解析;(2)点M的坐标为(﹣![]() ,
,![]() ).(3)y=x+4
).(3)y=x+4![]() .
.
【解析】
试题分析:(1)先根据AM=BM得出点M为AB的中点,再根据MC⊥x轴,MD⊥y轴,故MC∥OB,MD∥OA得出点C和点D分别为OA与OB中点,根据OA=OB即可得出结论;
(2)由(1)知,MC=MD,设点M的坐标为(﹣a,a).把M (﹣a,a)代入函数y=![]() 中求出a的值即可;
中求出a的值即可;
(3)根据点M的坐标得出MC,MD的长,故可得出A、B两点的坐标,利用待定系数法即可得出直线AB的解析式.
(1)证明:∵AM=BM,
∴点M为AB的中点
∵MC⊥x轴,MD⊥y轴,
∴MC∥OB,MD∥OA,
∴点C和点D分别为OA与OB中点,
∵OA=OB,
∴MC=MD.
(2)解:∵由(1)知,MC=MD,
∴设点M的坐标为(﹣a,a).
把M (﹣a,a)代入函数y=![]() 中,解得a=2
中,解得a=2![]() .
.
∴点M的坐标为(﹣![]() ,
,![]() ).
).
(3)解:∵点M的坐标为(﹣![]() ,
,![]() ),
),
∴MC=![]() ,MD=
,MD=![]() ,
,
∴OA=OB=2 MC=![]() ,
,
∴A(﹣![]() ,0),B(0,
,0),B(0,![]() ).
).
设直线AB的解析式为y=kx+b,
把点A(﹣![]() ,0)和点B(0,
,0)和点B(0,![]() )分别代入y=kx+b中,
)分别代入y=kx+b中,![]() 解得
解得![]() ,
,
∴直线AB的解析式为y=x+4![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目