题目内容
请将下面证明中的每一步理由填在括号内：
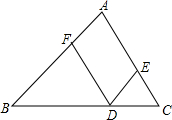
已知：如图，D，E，F分别是BC，CA，AB上的点，DE∥∠BA，DF∥CA．
求证：∠FDE=∠A．
证明：∵DE∥BA________，
∴∠FDE=∠BFD________．
∵DF∥CA________，
∴∠BFD=∠A________．
∴∠FDE=∠A________．
已知 两直线平行，内错角相等 已知 两直线平行，同位角相等 等量代换
分析：本题主要利用平行线的判定及性质就可填空，即同位角相等，两直线平行．内错角相等，两直线平行．同旁内角互补，两直线平行．反之就是性质．
解答：证明：∵DE∥BA （已知），
∴∠FDE=∠BFD（ 两直线平行，内错角相等）．
∵DF∥CA（ 已知），
∴∠BFD=∠A （两直线平行，同位角相等）．
∴∠FDE=∠A（等量代换）已知；两直线平行，内错角相等；已知；两直线平行，同位角相等；等量代换；
点评：本题主要考查了平行线的判定及性质，比较简单．
分析：本题主要利用平行线的判定及性质就可填空，即同位角相等，两直线平行．内错角相等，两直线平行．同旁内角互补，两直线平行．反之就是性质．
解答：证明：∵DE∥BA （已知），
∴∠FDE=∠BFD（ 两直线平行，内错角相等）．
∵DF∥CA（ 已知），
∴∠BFD=∠A （两直线平行，同位角相等）．
∴∠FDE=∠A（等量代换）已知；两直线平行，内错角相等；已知；两直线平行，同位角相等；等量代换；
点评：本题主要考查了平行线的判定及性质，比较简单．
练习册系列答案
相关题目
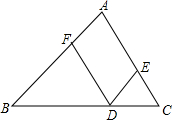请将下面证明中的每一步理由填在括号内：
请将下面证明中每一步的理由填在括号内：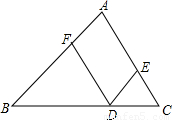
，
______
．______
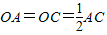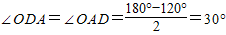