题目内容
一个圆内接正六边形的边长为2，那么这个正六边形的边心距为分析：根据正六边形的特点，通过中心作边的垂线，连接半径，结合解直角三角形的有关知识解决．
解答：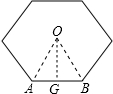
解：如图，连接OA、OB；过点O作OG⊥AB于点G．
在Rt△AOG中，OA=2，∠AOG=30°，
∴OG=OA•cos 30°=2×
=
．
故答案为：
．
解：如图，连接OA、OB；过点O作OG⊥AB于点G．在Rt△AOG中，OA=2，∠AOG=30°，
∴OG=OA•cos 30°=2×
| ||
| 2 |
| 3 |
故答案为：
| 3 |
点评：此题主要考查正多边形的计算问题，属于常规题．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目