题目内容
当x 时,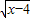 在实数范围内有意义;当x满足 时,等式
在实数范围内有意义;当x满足 时,等式 成立.
成立.
【答案】分析:根据二次根式有意义的条件得到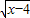 在实数范围内有意义,则x-4≥0,然后解不等式;根据二次根式的除法法则得到当等式
在实数范围内有意义,则x-4≥0,然后解不等式;根据二次根式的除法法则得到当等式 成立,则有x+4≥0且3-x>0,然后求出两个不等式的公共部分即可.
成立,则有x+4≥0且3-x>0,然后求出两个不等式的公共部分即可.
解答:解: 在实数范围内有意义,则x-4≥0,即x≥4;
在实数范围内有意义,则x-4≥0,即x≥4;
若等式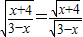 成立,则x+4≥0且3-x>0,解得-4≤x<3.
成立,则x+4≥0且3-x>0,解得-4≤x<3.
故答案为x≥4;-4≤x<3.
点评:本题考查了二次根式的乘除法: •
• =
=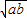 (a≥0,b≥0),
(a≥0,b≥0),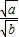 =
= (a≥0,b>0).也考查了二次根式有意义的条件.
(a≥0,b>0).也考查了二次根式有意义的条件.
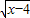 在实数范围内有意义,则x-4≥0,然后解不等式;根据二次根式的除法法则得到当等式
在实数范围内有意义,则x-4≥0,然后解不等式;根据二次根式的除法法则得到当等式 成立,则有x+4≥0且3-x>0,然后求出两个不等式的公共部分即可.
成立,则有x+4≥0且3-x>0,然后求出两个不等式的公共部分即可.解答:解:
 在实数范围内有意义,则x-4≥0,即x≥4;
在实数范围内有意义,则x-4≥0,即x≥4;若等式
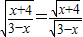 成立,则x+4≥0且3-x>0,解得-4≤x<3.
成立,则x+4≥0且3-x>0,解得-4≤x<3.故答案为x≥4;-4≤x<3.
点评:本题考查了二次根式的乘除法:
 •
• =
=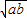 (a≥0,b≥0),
(a≥0,b≥0),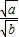 =
= (a≥0,b>0).也考查了二次根式有意义的条件.
(a≥0,b>0).也考查了二次根式有意义的条件. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
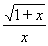
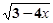 在实数范围内有意义.
在实数范围内有意义. 在实数范围内有意义.
在实数范围内有意义. 在实数范围内有意义.
在实数范围内有意义.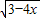 在实数范围内有意义.
在实数范围内有意义.