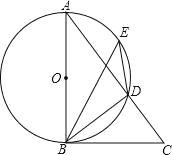
题目内容
【题目】如图1,AB是⊙O的直径,E是AB延长线上一点,EC切⊙O于点C,OP⊥AO交AC于点P,交EC的延长线于点D.
(1)求证:△PCD是等腰三角形;
(2)CG⊥AB于H点,交⊙O于G点,过B点作BF∥EC,交⊙O于点F,交CG于Q点,连接AF,如图2,若sinE=![]() ,CQ=5,求AF的值.
,CQ=5,求AF的值.
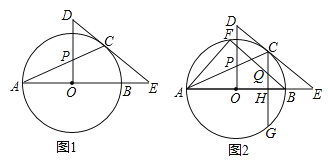
【答案】(1)证明见解析;(2)12.
【解析】
试题分析:(1)连接OC,由切线性质和垂直性质得∠1+∠3=90°、∠2+∠4=90°,继而可得∠3=∠5得证;
(2)连接OC、BC,先根据切线性质和平行线性质及垂直性质证∠BCG=∠QBC得QC=QB=5,而sinE=sin∠ABF=![]() ,可知QH=3、BH=4,设圆的半径为r,在RT在△OCH中根据勾股定理可得r的值,在RT△ABF中根据三角函数可得答案.
,可知QH=3、BH=4,设圆的半径为r,在RT在△OCH中根据勾股定理可得r的值,在RT△ABF中根据三角函数可得答案.
试题解析:(1)连接OC,∵EC切⊙O于点C,∴OC⊥DE,∴∠1+∠3=90°,又∵OP⊥OA,∴∠2+∠4=90°,∵OA=OC,∴∠1=∠2,∴∠3=∠4,又∵∠4=∠5,∴∠3=∠5,∴DP=DC,即△PCD为等腰三角形;
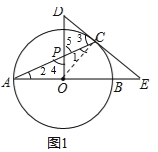
(2)如图2,连接OC、BC.∵DE与⊙O相切于点E,∴∠OCB+∠BCE=90°,∵OC=OB,∴∠OCB=∠OBC,∴∠OBC+∠BCE=90°,又∵CG⊥AB,∴∠OBC+∠BCG=90°,∴∠BCE=∠BCG,∵BF∥DE,∴∠BCE=∠QBC,∴∠BCG=∠QBC,∴QC=QB=5,∵BF∥DE,∴∠ABF=∠E,∵sinE=![]() ,∴sin∠ABF=
,∴sin∠ABF=![]() ,∴QH=3、BH=4,设⊙O的半径为r,∴在△OCH中,
,∴QH=3、BH=4,设⊙O的半径为r,∴在△OCH中,![]() ,解得:r=10,又∵∠AFB=90°,sin∠ABF=
,解得:r=10,又∵∠AFB=90°,sin∠ABF=![]() ,∴AF=12.
,∴AF=12.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目