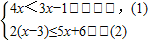题目内容
(2009•东城区一模)如图,梯形ABCD中,AD∥BC,∠B=45°,∠D=120°,CD=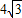 cm,求AB的长.
cm,求AB的长.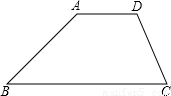
【答案】分析:如图,过点A、D分别作AE⊥BC、DF⊥BC,垂足分别为点E、F,这样把梯形分割成直角三角形和矩形.然后分别在两个直角三角形中解直角三角形,求出BE,CF,最后就可以求出AB了.
解答: 解:过点A、D分别作AE⊥BC、DF⊥BC,垂足分别为点E、F,(1分)
解:过点A、D分别作AE⊥BC、DF⊥BC,垂足分别为点E、F,(1分)
∠AEB=∠DFC=90°
∵AD∥BC,∠D=120°,
∴∠C=60°.
在Rt△DFC中,∠DFC=90°,∠C=60°,CD=4
∴DF=CD•sin60°4 ×
× =6.(3分)
=6.(3分)
易证:四边形AEFD为矩形.
∴AE=DF=6.
在Rt△AEB中,∠AEB=90°,∠B=45°,
∴ =6
=6 .
.
点评:此题考查了梯形的一种常用辅助线即作梯形的高线,把梯形转化成两个直角三角形和一个矩形,然后利用直角三角形的知识解题.
解答:
 解:过点A、D分别作AE⊥BC、DF⊥BC,垂足分别为点E、F,(1分)
解:过点A、D分别作AE⊥BC、DF⊥BC,垂足分别为点E、F,(1分)∠AEB=∠DFC=90°
∵AD∥BC,∠D=120°,
∴∠C=60°.
在Rt△DFC中,∠DFC=90°,∠C=60°,CD=4

∴DF=CD•sin60°4
 ×
× =6.(3分)
=6.(3分)易证:四边形AEFD为矩形.
∴AE=DF=6.
在Rt△AEB中,∠AEB=90°,∠B=45°,
∴
 =6
=6 .
.点评:此题考查了梯形的一种常用辅助线即作梯形的高线,把梯形转化成两个直角三角形和一个矩形,然后利用直角三角形的知识解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(2009•东城区一模)某商场用36万元购进A,B两种商品,销售完后共获利6万元,其进价和售价如下表:
求该商场购进A,B两种商品各多少件.
| A | B | |
| 进价(元/件) | 1200 | 1000 |
| 售价(元/件) | 1380 | 1200 |
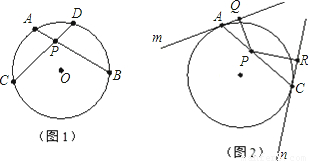
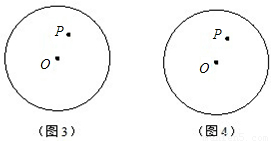
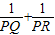 的值;
的值; 的值;
的值;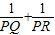 的值,并给出证明.
的值,并给出证明.