题目内容
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.
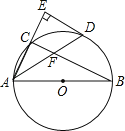
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长.
【答案】(1)ED与⊙O的位置关系是相切;(2)![]() .
.
【解析】
试题分析:(1)连接OD,根据∠CAB的平分线交⊙O于点D,则![]() =
=![]() ,依据垂径定理可以得到:OD⊥BC,然后根据直径的定义,可以得到OD∥AE,从而证得:DE⊥OD,则DE是圆的切线;
,依据垂径定理可以得到:OD⊥BC,然后根据直径的定义,可以得到OD∥AE,从而证得:DE⊥OD,则DE是圆的切线;
(2)首先证明△FBD∽△BAD,依据相似三角形的对应边的比相等,即可求DF的长,继而求得答案.
解:(1)ED与⊙O的位置关系是相切.理由如下:
连接OD,
∵∠CAB的平分线交⊙O于点D,
∴![]() =
=![]() ,
,
∴OD⊥BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
即BC⊥AC,
∵DE⊥AC,
∴DE∥BC,
∴OD⊥DE,
∴ED与⊙O的位置关系是相切;
(2)连接BD.
∵AB是直径,
∴∠ADB=90°,
在直角△ABD中,BD=![]() =
=![]() =
=![]() ,
,
∵AB为直径,
∴∠ACB=∠ADB=90°,
又∵∠AFC=∠BFD,
∴∠FBD=∠CAD=∠BAD
∴△FBD∽△BAD,
∴![]() =
=![]()
∴FD=![]()
∴AF=AD﹣FD=5﹣![]() =
=![]() .
.


练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目