题目内容
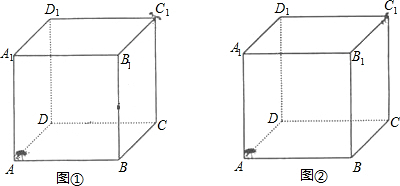
(2013•山西模拟)如图①,一个无盖的正方体盒子的棱长为10厘米,顶点C1处有一只昆虫甲,在盒子的内部顶点A处有一只昆虫乙.(盒壁的厚度忽略不计)
(1)假设昆虫甲在顶点C1处静止不动,在图①画出一条路径,使昆虫乙从顶点A沿这条路径爬行,可以在最短的时间内捕捉到昆虫甲.(请简要说明画法)
(2)如图②,假设昆虫甲静止不动,昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?
(3)如图②,假设昆虫甲从顶点C1,以1厘米/秒的速度在盒子的内部沿棱C1C向下爬行,同时昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?(精确到1s).参考数据:
≈4.4,
≈4.6.
(1)假设昆虫甲在顶点C1处静止不动,在图①画出一条路径,使昆虫乙从顶点A沿这条路径爬行,可以在最短的时间内捕捉到昆虫甲.(请简要说明画法)
(2)如图②,假设昆虫甲静止不动,昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?
(3)如图②,假设昆虫甲从顶点C1,以1厘米/秒的速度在盒子的内部沿棱C1C向下爬行,同时昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?(精确到1s).参考数据:
| 19 |
| 21 |

分析:(1)当相邻两个面放在同一平面内时,过AC1的线段必过公共棱的中点,按此方法,可画出A,C1所在的相邻面的所有公共棱的中点;
(2)根据昆虫甲静止不动,昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,得出AC1=
=10
cm,即可求出所行时间;
(3)联系(1)中的4个结论,分别画出图形,利用勾股定理求得两点间的最短路线,进而求解.
(2)根据昆虫甲静止不动,昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,得出AC1=
| 202+102 |
| 5 |
(3)联系(1)中的4个结论,分别画出图形,利用勾股定理求得两点间的最短路线,进而求解.
解答: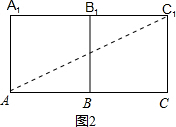 解:(1)画出图①中A?E2?C1,A?E3?C1,A?E4?C1中任意一条路径;(E1、E2、E3分别为各棱中点)
解:(1)画出图①中A?E2?C1,A?E3?C1,A?E4?C1中任意一条路径;(E1、E2、E3分别为各棱中点)
(2)如图2,根据昆虫甲静止不动,昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,
AC1=
=10
cm,
故昆虫乙至少需要爬行:10
÷2=5
秒,
答:昆虫乙至少需要5
时间才能捕捉到昆虫甲;
(3)由(1)可知,当昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙可以沿下列四种路径中的任意一种爬行:
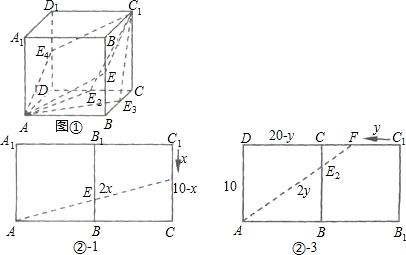
可以看出,图②-1与图②-2中的路径相等,图②-3与图②-4中的路径相等.
①设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E→F爬行捕捉到昆虫甲需x秒钟,
如图②-1-1,在Rt△ACF中,
(2x)2=(10-x)2+202,
解得x=10秒;
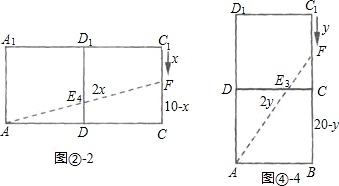
设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E2→F爬行捕捉到昆虫甲需y秒钟,
如图②-1-2,在Rt△ABF中,
(2y)2=(20-y)2+102,
解得y≈8秒;
所以昆虫乙从顶点A爬行捕捉到昆虫甲至少需8秒钟..
 解:(1)画出图①中A?E2?C1,A?E3?C1,A?E4?C1中任意一条路径;(E1、E2、E3分别为各棱中点)
解:(1)画出图①中A?E2?C1,A?E3?C1,A?E4?C1中任意一条路径;(E1、E2、E3分别为各棱中点)(2)如图2,根据昆虫甲静止不动,昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,
AC1=
| 202+102 |
| 5 |
故昆虫乙至少需要爬行:10
| 5 |
| 5 |
答:昆虫乙至少需要5
| 5 |
(3)由(1)可知,当昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙可以沿下列四种路径中的任意一种爬行:


可以看出,图②-1与图②-2中的路径相等,图②-3与图②-4中的路径相等.
①设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E→F爬行捕捉到昆虫甲需x秒钟,
如图②-1-1,在Rt△ACF中,
(2x)2=(10-x)2+202,
解得x=10秒;
设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E2→F爬行捕捉到昆虫甲需y秒钟,
如图②-1-2,在Rt△ABF中,
(2y)2=(20-y)2+102,
解得y≈8秒;
所以昆虫乙从顶点A爬行捕捉到昆虫甲至少需8秒钟..
点评:此题主要考查了平面展开图的最短路径问题,立体图形中的最短距离,通常要转换为平面图形的两点间的线段长来进行解决.

练习册系列答案
相关题目
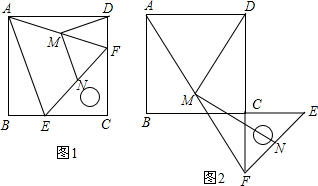 (2013•山西模拟)操作与证明:如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.
(2013•山西模拟)操作与证明:如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.