题目内容
【题目】如图,直线l1的函数表达式为y1=﹣3x+3,且l1与x轴交于点D,直线l2:y2=kx+b经过点A,B,与直线l1交于点C.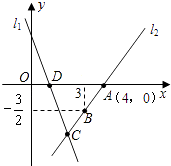
(1)求直线l2的函数表达式及C点坐标;
(2)求△ADC的面积;
(3)当x满足何值时,y1>y2;(直接写出结果)
(4)在直角坐标系中有点E,和A,C,D构成平行四边形,请直接写出E点的坐标.
【答案】
(1)解:∵点A(4,0)、B(3,﹣ ![]() )在直线l2:y2=kx+b上,
)在直线l2:y2=kx+b上,
∴ 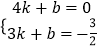 ,
,
解得: 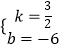 .
.
∴直线l2的解析式为y2= ![]() x﹣6;
x﹣6;
由 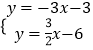 ,
,
解得 ![]() .
.
∴点C的坐标为(2,﹣3)
(2)解:∵点D是直线l1:y=﹣3x+3与x轴的交点,
∴y=0时,0=﹣3x+3,解得x=1,
∴D(1,0),
∵A(4,0),
∴AD=4﹣1=3,
∴△ADC的面积= ![]() ×3×3=
×3×3= ![]()
(3)解:由图象可知,当x<2时,y1>y2
(4)解:符合条件的E点的坐标为E1(5,﹣3)、E2(3,3)、E3(﹣1,﹣3),
①以AC为对角线时,
∵四边形ADCE是平行四边形,
∴CE∥DA,CE=DA=3,
∴将点C(2,﹣3)向右平移3个单位得到点E,即E1(5,﹣3);
②以AD为对角线时,
∵四边形ACDE是平行四边形,
∴CE与AD互相平分,即CE与AD的中点重合,则E2(3,3);
③以CD为对角线时,
∵四边形ADEC是平行四边形,
∴CE∥AD,CE=AD=3,
∴将点C(2,﹣3)向左平移3个单位得到点E,即E3(﹣1,﹣3);
综上所述,符合条件的E点的坐标为E1(5,﹣3)、E2(3,3)、E3(﹣1,﹣3)
【解析】(1)由题意可知直线l2经过点A,B,利用待定系数法建立方程组求解即可;由直线l1的函数表达式和直线l2的函数解析式联立方程,求解即可得出点C的坐标。
(2)先求出点D的坐标,再求出AD的长,然后就可以求出△ADC的面积。
(3)由点C的坐标为(2,﹣3),因此观察直线x=2左右两侧的图像,即可得出y1>y2时,x的取值范围。
(4)此小题分三种情况:①以AC为对角线时;②以AD为对角线时;③以CD为对角线时;根据平行四边形的性质就可以求出满足条件的点E的坐标。
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分)的相关知识才是答题的关键.

 阅读快车系列答案
阅读快车系列答案