题目内容
想一想，如何把图（1）变化得到图（2）如果AD∥BC，AD=BC，AE=CF，能判断△ADF与△CBE全等吗？请你说出下面思考过程中每一步的理由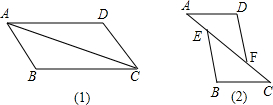
．因为AD∥BC，
所以∠A=∠C，这是根据
因为AE=CF，
所以AF=CE，这是根据
|
分析：显然∠A、∠C是内错角，则依据是两直线平行内错角相等，第二个是等式的性质，两边夹一角是SAS．
解答：解：（1）图（1）与图（2）比较可发现，将△ADC沿直线CA方向平移CF的长度即可得到图；
（2）∵AD∥BC，
∴∠A=∠C，
∵AE=CF，
∴AF=CE，
∴△ADF≌△CBE．
（2）∵AD∥BC，
∴∠A=∠C，
∵AE=CF，
∴AF=CE，
|
∴△ADF≌△CBE．
点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
练习册系列答案
相关题目
有一位老人担心自己百年以后，两个儿子为争夺遗产而不和．想着如何把自己的家业分给两个儿子，其中有一块地是平行四边形，地里有一口井，井的位置不在地的中间（如图）．老人想井不能分，两人可共用，但地要平分，老人想了很长时间，终于找到了分地方案．请你想一想老人的分地方案可能是怎样的（画在图上）？并说明理由．
如何求22.5°的正切值，小明想了一个办法：把一张正方形纸片（正方形ABCD）按如图方式折叠，使顶点B恰好落在对角线AC上，折痕为EC．根据小明的操作通过计算可以得到tan22.5°=
．
?△ADF≌△CBE，这是根据______．